这张试卷是今天上午做的,感觉出的比较诡异,总体来说难度不大,但是有几个题比较怪,比方说选择题的第七题,大题的第20题以及最后的那道线代大题,但是我做的并不好,出了很多失误,比如第一道极限题用泰勒给整错了,第21题的第一问也有个地方算错了,有个符号搞错了。。还是要稍微细心一些。
下面开始复盘:
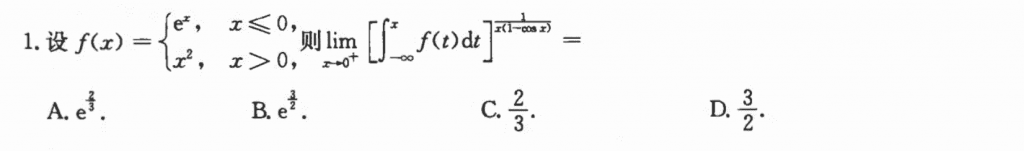
第一道就不那么“送分”,由于所给的被积函数是分段函数,因此就需要对这个变限积分进行分区间来确定$f(x)$,然后就能发现是$1^\infty$类型,三部曲就行了。
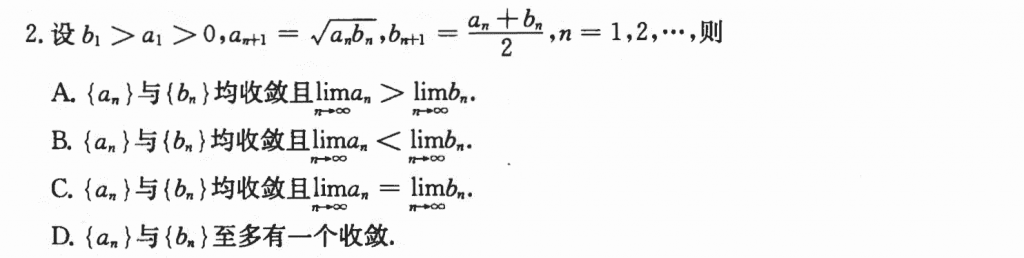
这道题主要是以前在880上做过,关键就在于意识到:$a_{n + 1} = \sqrt{a_nb_n} \le \frac{a_n+b_n}{2} = b_{n+1} $,然后后面就好整了。

基础题,直接判断就行
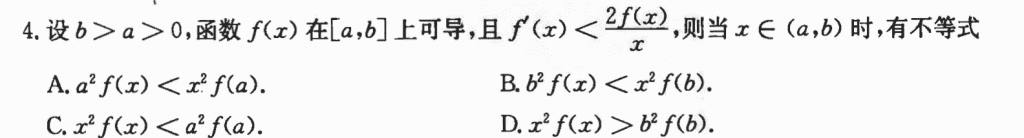
有点类似罗尔定理的证明题,找原函数,然后能知道原函数的单调性,再用单调性就能把不等式给弄出来。

$AC-B^2 > 0, A > 0$,就能知道充分条件了。
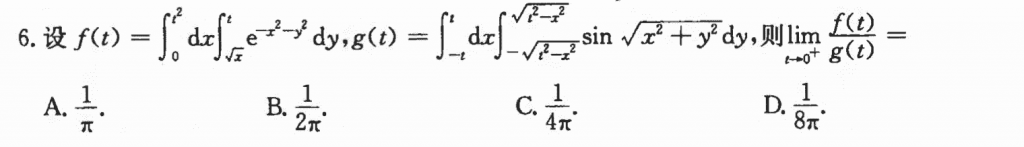
这道题我又想用二重积分的中值定理来做,但是不知道为啥搞不出来,然后就走洛必达的方法,第一个交换次序还好说,第二个我确实没想到转极坐标,蒙了个B还蒙对了。
可以积累一下这道题对$g(t)$处理的手法,之前确实没咋见过
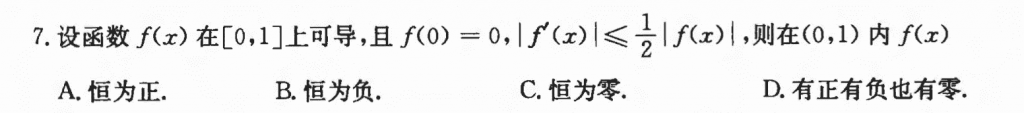
这道题比较难,用拉格朗日迭代,然后夹逼,之前也没有怎么见过,其实这道题有一个比较小的细节就是对$x$的放缩,我感觉这个很难想。
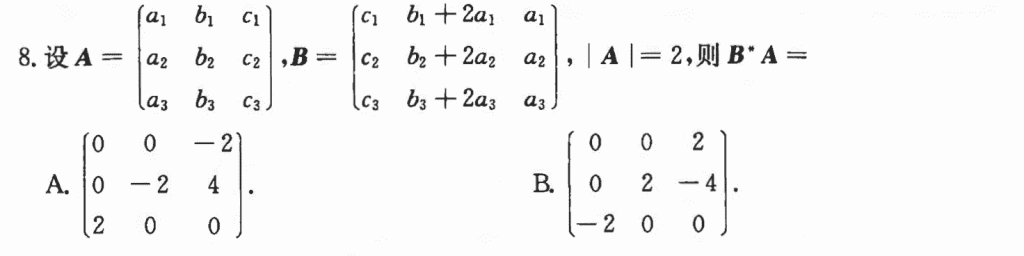
这道题比较简单,用初等变换把B写成A和初等矩阵相乘的形式,然后带进去就行了

$|A| = 0$实际上就可以说明$A$有个0特征值,然后$AB = -B$,然后$B$的列向量是满秩的,就可以说明A有三个特征值-1,然后B的列向量就是对应的特征向量。
然后用相似就能知道$2A + E$的特征值,那么行列式也就出来了
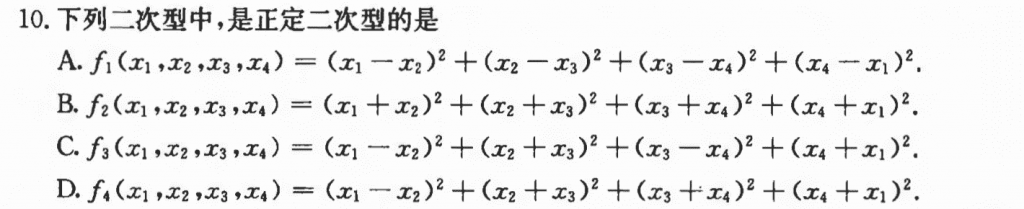
所给选项都是平方和,那么就说明这些二次型都是大于等于零的,那么任务就是要排除等于零的情况,因为正定的要求是绝对大于,就是把括号里面的东西单独摘出来,构造一个方程组,如果方程组只有零解,那么当$x \ne 0$的时候,对应的二次型就不等于零,只能大于零。
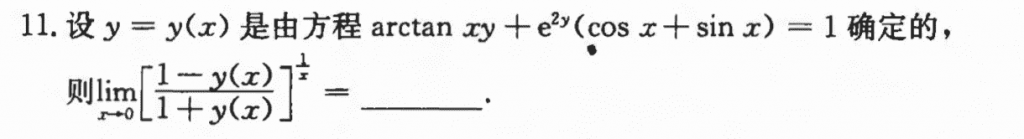
$1^\infty$新花样,本质还是那些玩意
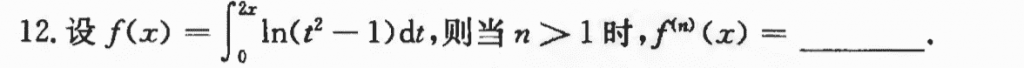
这道题我没做出来。。不太敢尝试,果然还是暴力求导+找规律

这道题挺麻烦的,要先把曲率表示出来,然后暴力求导,这个求导的过程有点麻烦,然后就找驻点判断极值点啥的。
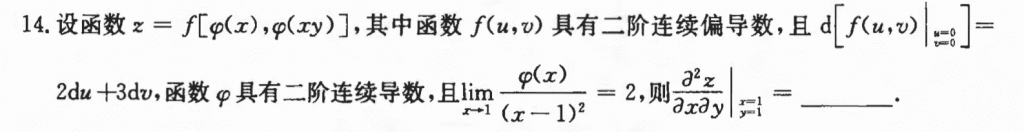
这道题先对$y$求偏导,然后把$y = 1$带进去以后,再对$x$求导会稍微方便一些。
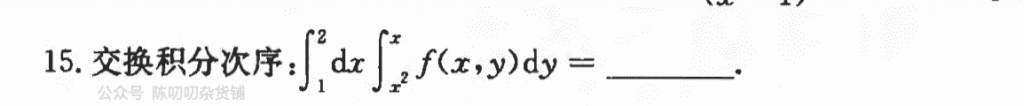
这道题基本白给,要注意串线时候的方向,确定符号

$B$的列向量是$A$取特征值-2时候对应的特征向量,那么也就说明负特征值的个数有$r$个,$C$也是同理,可以知道有$n-r$个,然后规范型就出来了。

泰勒,洛必达都行,基础题,结果我泰勒都泰错了。。
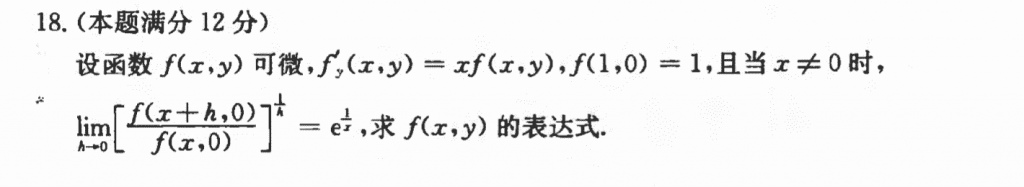
这道题感觉还是有点东西的,主要是不要被偏导给迷惑,本质其实还是一阶线性齐次微分方程,套公式就好。
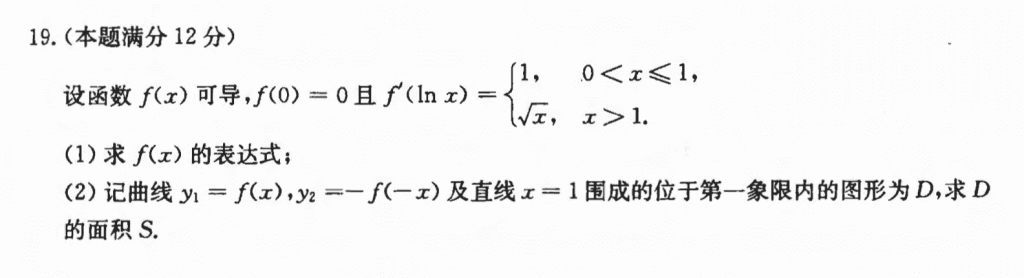
这道题第一问就换元,然后积分,然后根据连续性把常数给确定下来。
第二问也白给,套公式就好了

感觉这道题放到这里。。挺恶心人的,这计算量是真有点大。
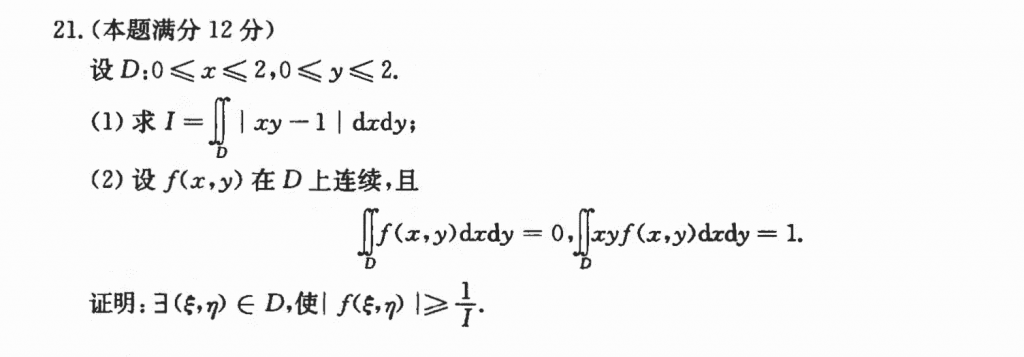
第一问比较基础,但是我给整错了个负号,血亏。。
第二问和21年李艳芳三套卷里头的一道题基本是一样的:https://www.vsbf.fun/archives/2037,第二套的第二十题,当时的解析给的是闭区间的连续函数,然后放缩来做的,我当时就整的二重积分中值定理,还不能确定对不对,结果这道题的解析就是用的就是二重积分的第一中值定理,挺好的。

这题pass了,有点过于偏难了。。







Comments NOTHING