这张试卷是今天下午做的,昨晚没睡好,上午睡到九点多才起来,所以就只能下午模拟了。。上午起来整了杯咖啡,结果中午午觉又没睡着,下午做卷子还挺懵逼的,这套卷子计算量依旧很大,再加上状态不太行,做的比较痛苦,客观评价这张试卷,我感觉小题还好,当然也是很有难度的,大题计算量也比较大的。
下面开始复盘:
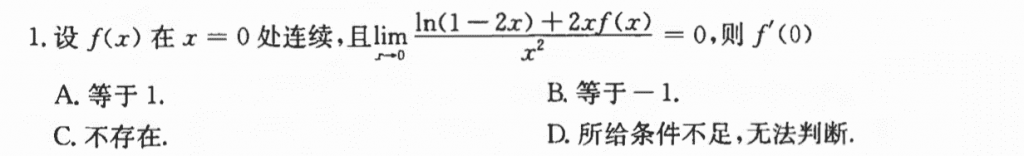
比较基础,直接泰勒或者加项减项拆都可以
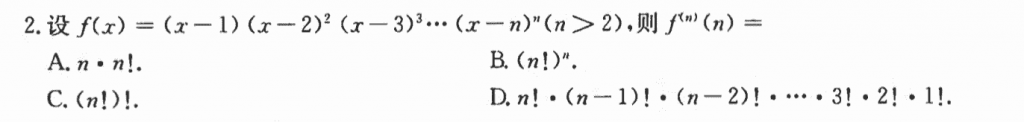
要求$f^n(n)$,那么实际也就是要求:$n!\times a_n$,其中$a_n$是函数归幂之后$(x - n)^n$前的系数,而题目所给的函数里面的已经有了$(x - n)^n$,那么就只需要把$n$带到前$n - 1$项中就得到$a_n$了。
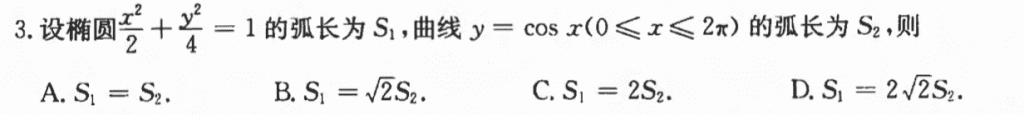
这道题难度也不大,先把弧长都表示出来,然后就能找到关系,有个定积分不用计算。

比较麻烦的概念题
推导的方法都是用导数定义+洛必达,其中第一个可以积累一下当成一个结论来记
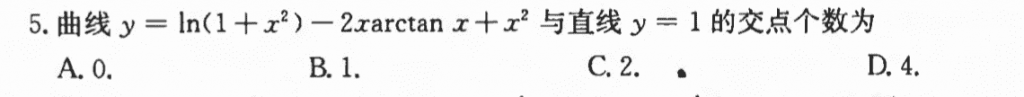
这道题做错了,忘了考虑$x < 0$的情况。。算出来是单调递增的还以为就一个交点。。还是不够细心。。
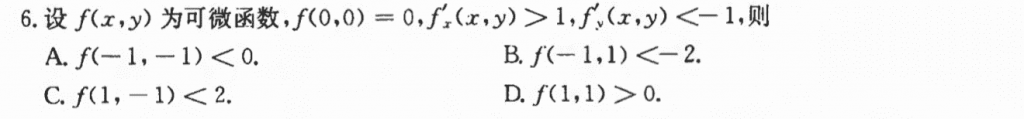
其实我做这种题都是靠脑补一个坐标系来做,导数表示的是变化率,比方说$f'_x(x, y) = 1$,那就是说在$x$轴方向上移动一个单位,那么对应的$f(x, y)$就会移动一个单位,同理$y$方向也是,那么就能大概推出来选B,然后再用拉格朗日放缩验证一下就好了。

这道题也错了,主要是比较I和K的时候,确实没想到作商,还想了很久。。
比较J和K可以直接相减,然后用单调性的方法,I和J就作商,已经很久没用作商的方法了,生疏了。

A的任意两个特征向量都相关,那么可以说明几个东西:
- A的特征向量秩为1
- A只有一个三重特征值
- $3 - r(\lambda E - A) = 1$
然后就能确定$a$和$b$的取值了
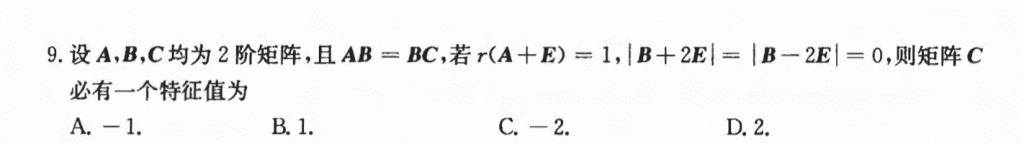
实际上这个$|B+2E| = |B-2E| = 0$就是为了说明$B$是可逆的,然后就能推出$A$和$C$相似,已知了A的一个特征值,那么C的特征值也就出来了。

这道题是一道好题,首先给的二次型矩阵是不对称的,那么就需要构造对称的二次型矩阵:$A = \frac{1}{2}(A + A^T)$,这样二次型的矩阵就出来了,然后根据秩为1,就可以把a的值给整出来。然后在求规范型的时候,好像答案和哔哩哔哩的一些博主都直接算的特征值,其实这道题用配方法比较快,像这种只用判断特征值符号,而不用具体的特征值的题,尽量用配方法,所以需要多练一些。

首先根据斜渐近线,就能把$a$和$b$给整出来,还是建议这种填空题用朴素点的方法,也就是算两个极限的方法,因为填空题对答案的要求很精确,选择题还可以比对选项,大题还有过程分,填空题一个数字不对就寄了,所以还是慢点。
然后这道题的话,这个定积分真的给的挺温柔的,可以来感受一下李正元的压迫感:


这道题其实不用整那么复杂,我一开始也没想出来,主要是确实感觉有些无从下手,都准备放弃了,结果突然就想到了$2x$和$x^2$的关系,就想能不能抵消啥的,然后就把$2x$凑到了后面的那个$d$里头,然后根据分子拆开:$$\int \frac{x^2}{1+cosx}dx + \int \frac{sinx}{1+cosx}dx^2 = \int \frac{x^2}{1+cosx}dx + \frac{x^2sinx}{1+cosx} - \int \frac{x^2}{1+cosx}dx$$
然后记得要加C

交换次序老朋友了,答案烧掉,不知道在整啥玩意
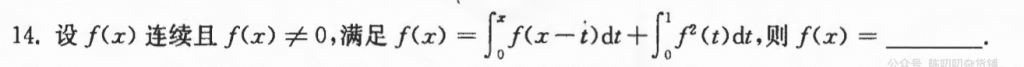
基本题,求导后转换为微分方程,然后确定常数就好了。
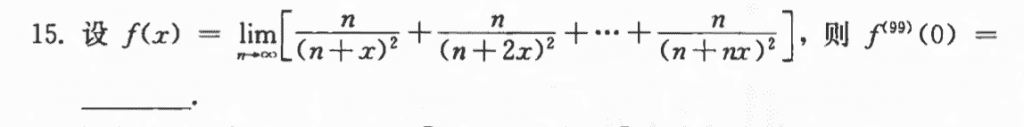
先用定积分的定义,可以把$f(x)$给求出来,然后要求$f^{(99)}(0)$,那么也就是$99! \times a_{99}$,其中$a_{99}是将$f(x)$归幂之后$x^{99}$前的系数,但是我没记$\frac{1}{1 + x}$的展开,这个数一的级数要求的。所以就用比较朴素的方法,多求几阶导,然后找规律。

公共解问题,$k_1\alpha_1 + k_2\alpha_2 = k_3\beta_1 + k_4\beta_2$,然后移项转化为方程组解的问题就能把$k_1, k_2$整出来,然后把$\xi$用$\alpha_1, \alpha_2$表示出来就好了。

这题的计算把我给整麻了,我没有用公式计算,用的是武忠祥辅导讲义上例题的方法,不得不说计算量真的大,答题卡都写不下了。。

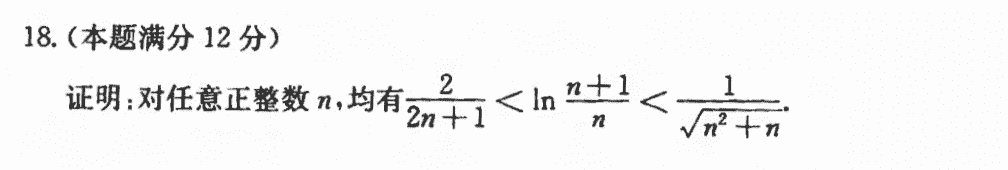
这题没整出来,确实没想到换元$x = \frac{1}{n}$,后面就构造函数,然后用单调性就好了。

这道题比较简单,这种函数方程一般都直接用导数定义来建立微分方程,然后求解微分方程就好了,第二问的二重积分难度也比较小,用极坐标算就行了。
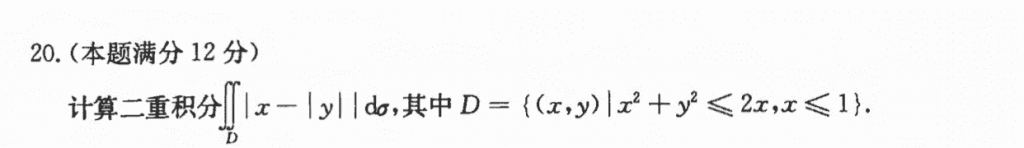
画图之后是关于$x$轴对称的,然后被积函数里头是关于$y$的绝对值,所以可以把区间缩小一半,然后套在$y$身上的绝对值也可以去掉,再分区间去掉$|x - y|$的绝对值就好了,在计算的时候三角形区域用直角坐标很简单,另一部分我一开始是用直角坐标,然后卡在了一个地方积分整不出来,然后就果断转极坐标了,计算量也不小。
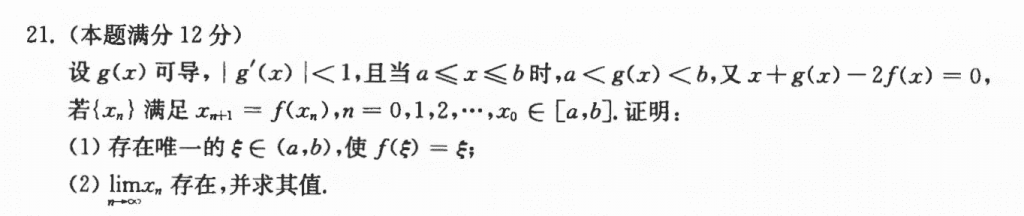
第一问和上一套那个压轴题基本是一样的,第二问的话我没想到用单调有界,还以为是像上一套那样用先斩后奏的方法,然后就用的先斩后奏。

这道题也很简单,用$B$作为过渡矩阵,建立$A$与对角矩阵的关系,然后$P$矩阵就可以整出来了。
第一问因为我打印的不清楚,还以为是要求$A^n - 6E$的秩,整了好久。。
如果是$A^* - 6E$的话那就比较简单,一连串的相似就行了。
复盘结束,码字较快,有什么问题欢迎在评论区与我留言,感谢阅读!







Comments NOTHING