这套卷子是今天上午做的,三个小时拉满,总体来说难度和前几套差不多吧,这套的选填思维难度不大,但是计算量不小,有几个大题的难度有点高,比如那道$ln$比大小的题目,还有微分方程的物理应用,基本都没什么想法。
下面开始复盘:

这道题直接对四个选项用拉格朗日就好了,比如A选项:$2^{\alpha(x)}-2^{\beta(x)} = 2^\xi ln2(\alpha (x) - \beta (x))$,其他几个选项也用相同的办法验证很容易推出选D

第二题难度不大,但是没见过这种的话估计就挺难搞的,主要是以前在880上遇到过,需要用个换元,然后构造方程组,把$f(x)$给整出来,然后再求导什么的就好了。

这道题答案还给错了,应该是选既非充分也非必要条件,我也是听哔哩哔哩的一个up才意识到对于洛必达的使用,传送门
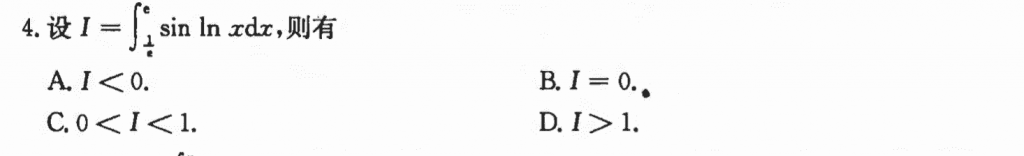
难度还是有些的,我乱做做出来了,就直接对sinlnx放缩,然后积分啥的
正统的方法是要先意识到在这个区间内sin有正有负,那么就需要把这两个区间分开(这并不是一个很新的思维方式,大家之前做三角函数比较大小肯定或多或少都接触过,不过那个地方的换元一般会涉及到三角函数的诱导公式),让正数和负数泾渭分明,然后再将它们利用换元的方法转换到同一个区间,然后比较被积函数就好了。
其实这道题我感觉答案还是有点问题,它证明的是被积函数是在0和1之间,但是外面还有个积分,这个积分的区间明显大于1了,不知道是不是有什么手法可以直接判断。

计算量挺大的一道题,先分段把$f(x)$整出来,然后再套公式算,说着简单,但是计算量是真不小。
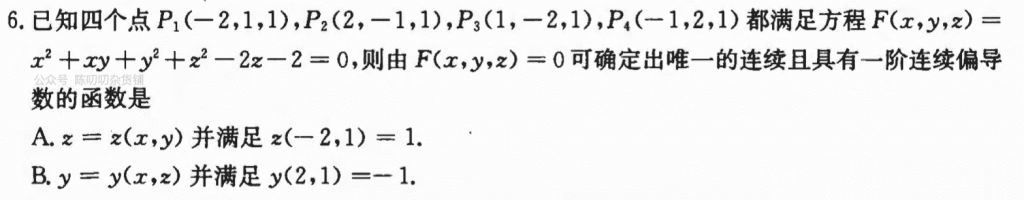
隐函数存在性定理,我感觉还是相对来说有点冷门的,比方说如果$z$是$x$,$y$的函数,那么$z$对$x$的偏导以及对$y$的偏导应该是都不为零的,这样的话才能说$z$是$x$,$y$的函数,然后验证选项就好了。

也比较简单,根据$y = x$可以知道通解的形式是:$y = (C_1 + C_2x)e^{0x}$,根据$y = xe^{-2x}$可以知道通解的形式:$y = (C_1 + C_2x)e^{-2x}$,那么也就说明0和-2是两个重根,然后就可以构造特征方程,再根据特征方程就能把微分方程推出来了。

这道题感觉还是比较简单的,答案用的是秩的方法来推,现在我用向量组相关无关的语言来描述一下。
首先如果$|A, \beta| = 0$,那么也就是说这个列向量组是线性相关的,但是这个向量组相关并不能一定推出$\beta$一定可以由$A$的列线性表示,所以充分性不满足。
如果$Ax = \beta$有解,那么也就是说$\beta$可以由$A$的列向量线性表示,那么也就可以推出向量组相关,对应的行列式就为零,所以必要性是满足的。

比较基础的题,就那些公式变就好了,可能求出来是$\frac{2}{3}A^{-1}$,再把它转换一下就得到B的结论了。

看到这个$A^*$,那么就需要考虑怎么对他进行出来,比如把他的特征值算一算啥的,总是需要试探的,然后发现好像什么也整不出来,那么就开始往别的方向考虑,比方说$AA^* = |A|E$,然后就能把$A^*$消去,右边部分就用特征值特征向量的定义,然后就能把$x$给整出来了
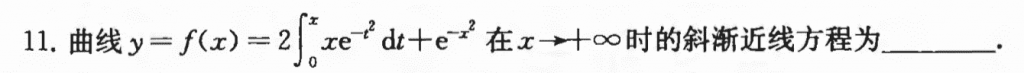
和前几套的某个大题如出一辙

难度也不大,先根据极值处导数值为零把a给整出来,然后再求二阶导判断凹凸区间。

看到被积函数里头有$e^x$,然后积分区间是对称的,那么就肯定想到区间再现,然后两个相加除2就能把$e^x$消去,再积分就好了。

这道题还是需要操作的,根据所给条件,比方说先把$y = 0$,带到$f(x, y)$里头,然后就能得到一个方程,再用偏导的条件啥的,就又能得到一个条件,其实这两个条件大概就能把$u(x)$给推出来了。答案还对$f(x, 0)$对$x$求了导,这确实是我没想到的,这样就更方便了。
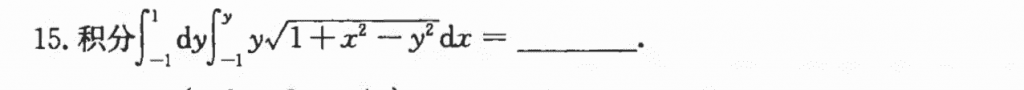
交换次序老朋友了,但是这道题有一个细节:$(x^2)^\frac{3}{2} = |x^3|$,这个绝对值很细节,不然算出来肯定和我一样是$\frac{2}{3}$

方程组问题,比较基础。

看着难,实际上是paper tiger,sin那个可以用下等价无穷小,然后后面就凑导数定义,就能得到微分方程,然后发现是一阶线性其次,直接套公式就行了
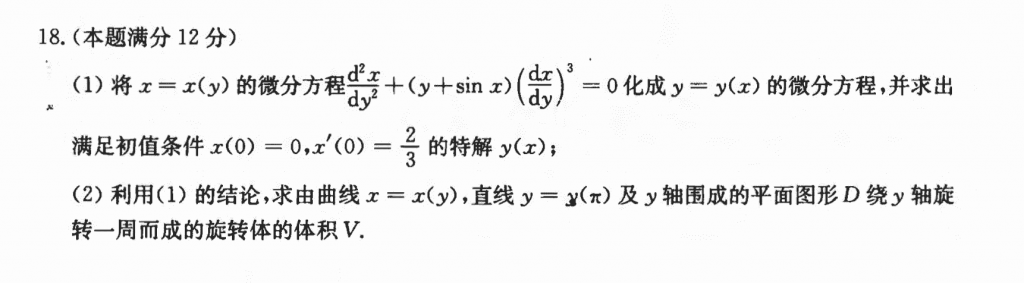
也没什么难度,pass了
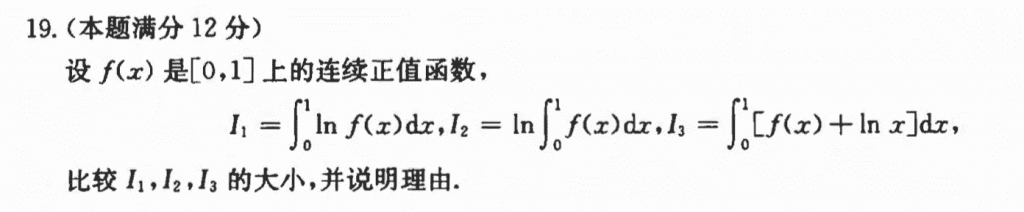
$I_1, I_2$的比较很麻烦,但是可以得到他们都是小于$I_3$的,对他们用一个放缩就好了
$\int_{0}^{1} lnf(x)dx \le \int_{0}^{1}f(x) - 1dx = I_3$
$ln\int_{0}^{1} f(x)dx \le \int_{0}^{1} f(x)dx - 1 = I_3$
然后$I_1, I_2$的比较是真不会。。
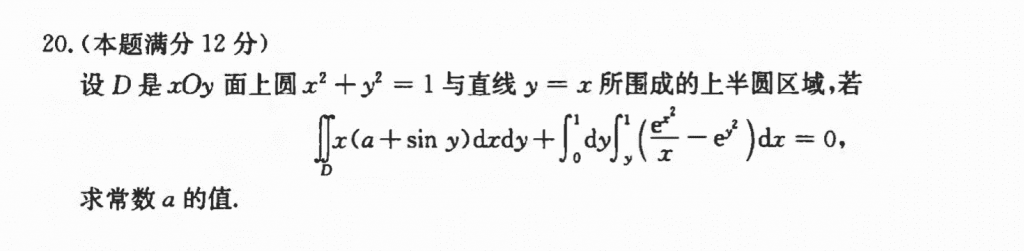
好题,需要算两个二重积分,都有技巧。
比如第一个二重积分,可以作一条辅助线$y = -x$,然后根据对称性就可以快速化简
对于第二个积分,需要把被积函数的这两个东西分开,然后第一个积分先对$y$积分再对$x$积分,第二个先对$x$再对$y$积分,就能发现他们之间有积不出来的东西是可以被消掉的。
然后就简单了。

不准备研究了,放了

这道题比较基础,第二问在求二次型矩阵的时候还是建议用初等变换的方法,比较快。
然后第三问实际上可以直接在第一问的基础上进行,再进行一个换元,把2怼到平方里头就好了。
八套卷总结
不得不说我感觉这八套卷子出的还是很棒的,小题兼顾了计算量和思维,大题的创新性也不低,除了有一些题目确实出的比较偏比较拉,感觉没有什么研究的含金量,直接放了就完了。
如果时间有限的话,可以只做选择题和填空题,因为感觉出的确实挺好,大题的话,线代部分要么就是太偏,比如第七套的那个AB乘积可交换;要么就是出的比较常规,比如这一套的线代题。
总之做这八套卷子我感觉对我的计算水平的提升很大,虽然还是会经常出现一些比较低级的错误,比如漏个符号什么的,但是相比之前来说好太多了。
之后还是需要对这八套卷子再多复盘复盘,毕竟认识过程具有反复性和无限性hh,肯定还是有些东西是没有挖掘出来的,加油了!







Comments NOTHING