这张卷子是昨天上午做的,机构组织了模拟考试,本来是考政治,我把数学卷子带去写了hhh,有点考场的感觉,毕竟去年的主要原因就是考场状态实在是太差了。
这套卷子我感觉很难,和上一套试卷不一样,这套卷子的选填不难,但是大题直接把我给送走了,好几道证明题,都没怎么做出来,需要专题突破了。
下面开始复盘

第一题不难,直接根据单调性分析,在$[0, \frac{\pi}{2}]$,$sinx$是单调递增的函数而$cosx$是单调递减函数,然后再根据基本不等式$sinx < x$,很快就能把答案选出来了。

第二题也不难,任意阶可导,这个函数的性质就很强了,所以直接常用的拐点和极值点的判断方法就可以把答案选出来。
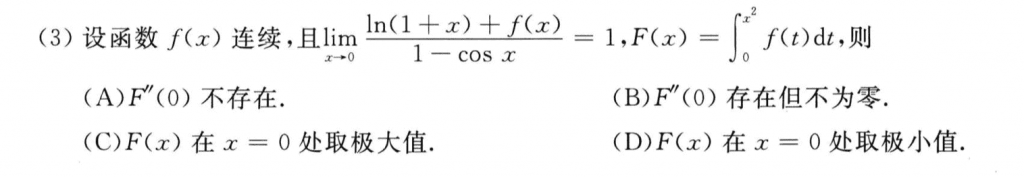
这个题我做错了,对着$F(x)$一直求导,中间估计有哪一步求错了,选了个B。。这题我感觉还是挺有意思的,求出$F'(x) = f(x^2)2x$之后,从前面那个极限可以知道$\lim_{x \to 0^+}f(x) <0$,然后$F'(x)$的单调性就由x决定了,可以知道在$x = 0$两侧$F'(x)$是异号的。

这题简单,1和2总有一个是错了,所以必不可能在一起,然后答案就出来了。
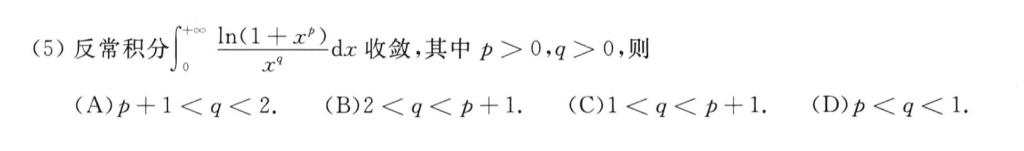
首先考虑$x \to 0$的情况,这个时候可以根据同阶同敛散进行等价无穷小化简,然后得到一个不等式,再考虑$x \to \infty$,这个时候ln其实没啥用了,只需要对$q$分析即可。

基本题,取极限

基本题,极值点判断出来以后,是否是最值还需要和边界上的点作比较。

这个题也不难,主要是根据下面这个性质:

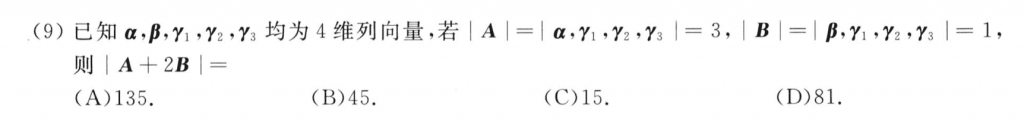
基础题,李永乐的线代强化讲义上好像都有这道例题

发现左右两个矩阵不是可逆的关系,也不是正交矩阵,那么就不能相似了,只能合同
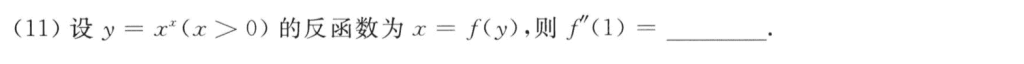
用反函数二阶导数的公式,这个公式要记

先转成直角坐标,然后可以根据对称性(特殊对称性x = 1)消去一部分,然后就好做了
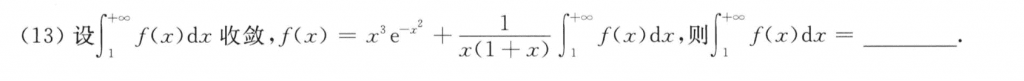
常规套路题,把这个要求的定积分设为一个字母,然后两边积分就好

这题题目我看错了。。不知道怎么就看成求面积了,没看到是旋转面的,不过也不难,套公式就好了,那个ds要用参数方程的形式带入
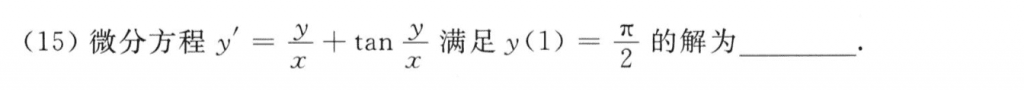
这题不难,设$u=\frac{y}{x}$就好

二重特征值,并且可以对角化,那么c要么是1要么是2,然后就看分别能不能提供三个无关的特征向量,如果可以那么就可以对角化
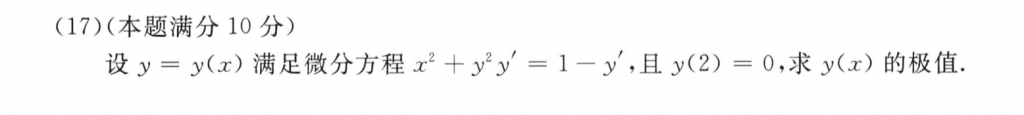
这个题直接根据所给的这个式子就能判断极值,我还求了个二阶导数来判断,慢了。
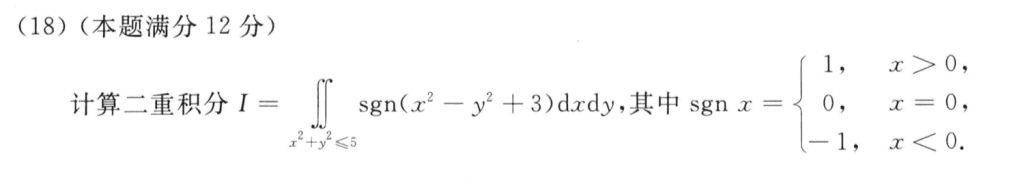
这题难,首先要知道那个sgn里头的函数是一个关于x轴对称的双曲线,然后分块来分析符号,最后一步算那几个积分很恶心,答案好是直接套的公式,虽然说这玩意在考场上也可以推,但是还是直接记好点,不然在考场上推挺浪费心情的。
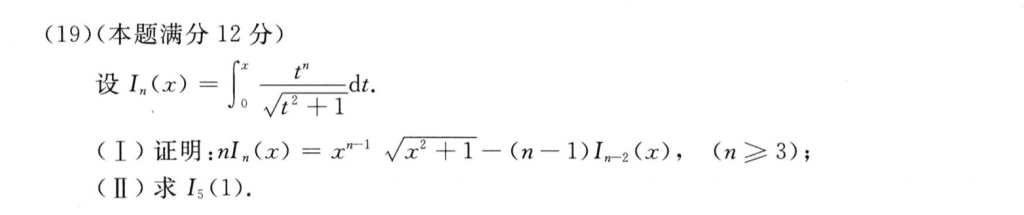
这个题我感觉也不简单,这一步真是逆天,我想破脑袋也没想出来还能这样操作。。
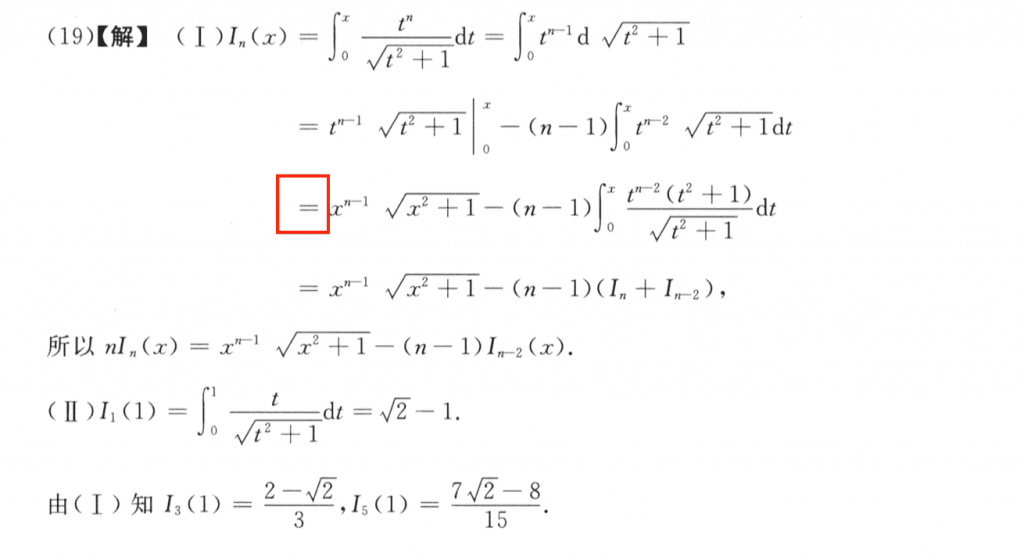

这个题比较难的点就在于根据一个点的二阶导数的符号,以及二阶导数连续,来判断这个点领域附近的凹凸性,去年考了个选择题,考场上真不知道这个知识点,五分直接白给了。。
第二问就在于要用放缩来推$f'(1) < 0$,答案给的方法我没想到,我放缩是用第一问求的极值来放缩的,因为在$x=0$处取极大值:$y(1) < y(0)$,也不知道有没有什么问题。
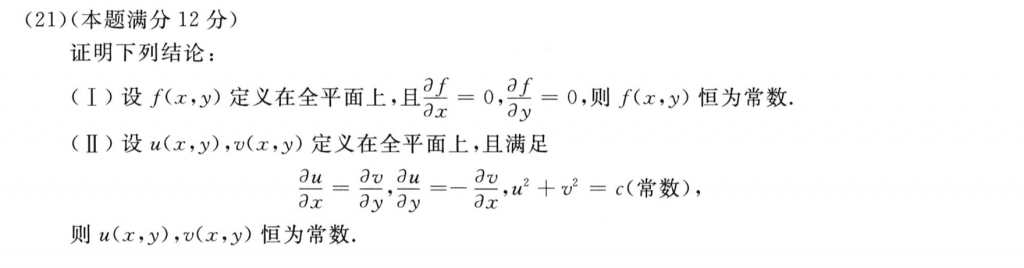
这个题我感觉也挺麻烦的,真没想到第一问就是要证明$f(x, y) = f(0, 0)$,然后拉格朗日两次就出来了,第二问就是要证明$\frac{\partial u}{\partial x} = \frac{\partial y}{\partial y}=0$,我觉得能把问题转化成这两个那么这道题就不难了。。想了半天的什么全平面。。
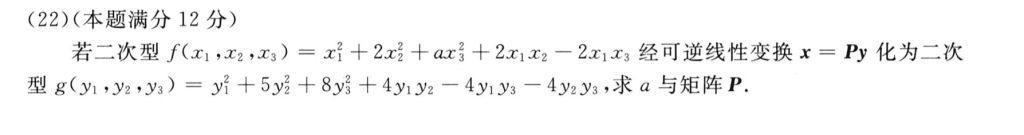
这题我感觉还是挺麻烦的,分数扣光,主要是忘了这个可逆线性变换不一定是相似的关系,我直接迹相等把a求出来,但是是错的,还是要根据秩来判断。
求矩阵p就需要用配方法画标准型,然后用这个标准型作作为过渡来联系$f(x_1, x_2, x_3), g(x_1, x_2, x_3)$
这题我觉得可以作为平常学习的例题,挺好的,我做这种题太少了,今年感觉考的可能性挺大的。
复盘结束,码字较快,如果有什么问题欢迎在评论区留言,感谢阅读。







Comments NOTHING