这套试卷是昨天下午做的,本来机构组织考英语,我又把数学卷子拿过去写了hh
客观评价这套卷子,我感觉难度比前一套小了很多,我两个小时就写完了,现在开始复盘:

第一题这道题应该是挺简单的,首先AB是$sin\infty, cos\infty$,那么肯定是摆动的,不可能收敛,然后在C和D里面选,其中D应该是很好判断的,提个$3^n$到根号外面,就出来了。
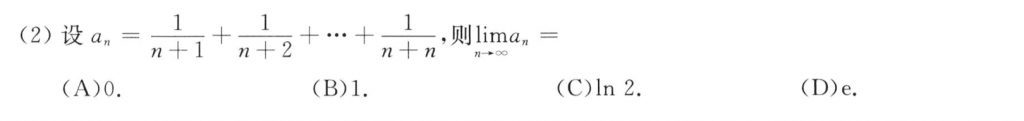
第二题就定积分的定义,基础题

这题我做错了,感觉每次遇到微分方程+周期的题我都会做错。。我主要是对他这里的有周期解理解有问题,还以为所有的解都要是周期的,没想到是存在,那么在$a \ne b$的时候,只需要让$C_1, C_2 =0$,那么就有周期解了。
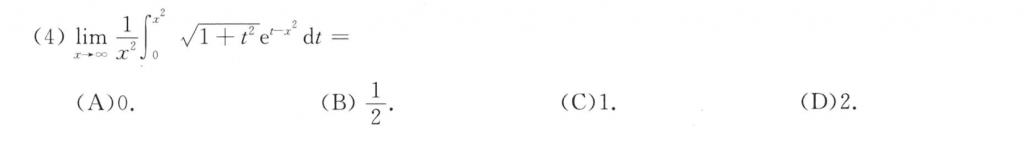
这题也不难,把那个定积分里头的$e^{-x^2}$挪到外面去,然后洛必达就行了。
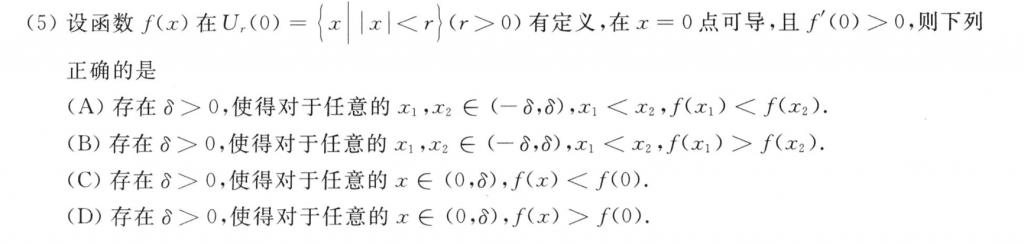
$f'(0) > 0$,没有在一点导数连续的条件,那么就只能推出在这点左边的点比$f(0)$小,右边的比$f(0)$大,至于他们这些点之间的单调性实际上是不能知道的。

这题感觉做过好多遍了,基础题。
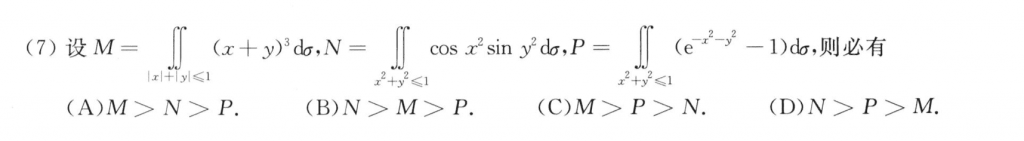
M是奇函数,可以很快推出它等于零,N的话$x^2$和$y^2$都大于零,那么N也大于零了,P就很快可以推出来是小于零的。

这题AB实际上很好判断是正确的,主要是C和D,实际上,因为$\beta$的任意性,可以直接设$\beta = -\alpha_1$,那么就可以很快把D排除了。

只有$A+B$才能保证$A+B$的特征值都是大于零的,所以是正定

A是可以对角化的,如果要和A相似,那么选项中的矩阵应该都要可以对角化,就考察是否有三个无关的特征向量就好了。

直接两边微分,然后变形就挺简单的,应该是武老师讲义上的原题
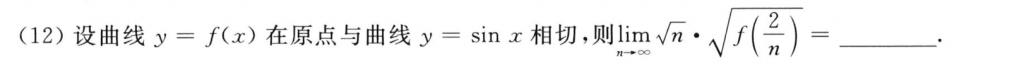
这题也不难,那个极限就凑导数定义

这题我感觉挺难的。
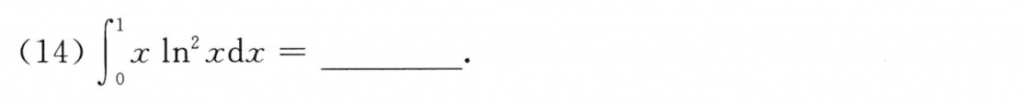
反复分部积分就好了

基础题,去年好像就考了个超过二阶的微分方程的题目。

$\alpha\alpha^T$的特征值就是1, 0, 0

直接换元,令$x = sint$,然后这个积分的计算就挺简单了。

这题660上好像有一样的,比较基本的题。

拿到这种什么极值、单调、凹凸、拐点的题第一步一定是要判断奇偶性的,这样可以减少一半的工作量,我想判断奇偶性,但是有个点没想通,奇偶性没判断出来,所以就直接硬求了,挺麻烦的。
第二问就套公式,但是因为是偶函数,所以左右两部分旋转出来的东西会重合,不要求多了。

这题我感觉也难,主要是对原点对称的手法不太熟悉,然后去哔哩哔哩补了一下之后清晰了不少。

这题用到了广义的罗尔定理:$f(0) = f(\infty)$,也是可以用罗尔定理的

直接初等变换把A和B拼在一起,然后A作初等行变换,对B也做同样的变换,当A变成单位矩阵的时候,B就变成了P,不过这道题要注意一个细节就是P是可逆的,所以需要对任意常数作一个约束,来保证可逆。







Comments NOTHING