做题时间:今天中午12.30-15.00,上午睡了一上午,所以下午才写这套卷子。。
做题的感受就是比2006年压力会稍大一些,主要难在计算量上,然后证明题我感觉也有些难,没有做出来。一共错了一个填空题,证明题只写了两个最大值在同一点取的情况,然后二重积分最后算的那个结果掉了个绝对值。
下面开始复盘

第一题比较基础,比较好排除ACD,对于B选项,我复盘的时候才发现做错了。。但是还选对了,我把1+x看成了1-x,然后直接用那个平方差公式就出来了。

第二题也比较基础,依旧考察$e^\infty$

经典题,许多习题册、讲义上面都有,首先观察图像发现是奇函数,那么$F(x)$就是偶函数,$F(3)$和$F(2)$正负性是相同的,然后$F(3)$会稍微小一些,就可以选出来了。

D选项就很好选出来,武忠祥强化课讲过分子上是两个变动的函数相减不能推导数存在,反例就是$y=|x|$

依次分析水平、垂直和斜渐近线就好了,然后不要走弯路,比如如果一个函数的一侧有了水平渐近线,那么这一侧就没有斜渐近线了。

折磨题,如果要正面证明的话,难度相当大,我用的是画图的方法,图像的方法就比较简单了,可以画一个凹函数,然后选取点,依次排除ABC就好了。
正面的证明要用拉格朗日,然后构造一个式子,挺麻烦的,不过可以积累一下这个手法。

第七题我主要是以前做过,因为做错过,所以印象深刻,首先其实C挺有迷惑性的,咋一看还以为是错了,因为没有偏导,但实际上根据这个极限的式子是可以推出(0, 0)点的两个偏导都是零的,比如要求对x的偏导,直接把y=0带进去,然后分母变成了x的绝对值,用一个换分母的手法:
$$\lim_{x \to 0}\frac{f(x, 0)-f(0, 0)}{|x|}=\lim_{x \to 0}\frac{f(x, 0)-f(0, 0)}{x}\times \frac{x}{|x|}=0$$
然后后面那个部分是有界的,然后极限存在,所以对x的偏导那个部分就是零了。
然后D的话,可微的一个充分条件是偏导连续,是一个二元极限,这个是单侧极限,和偏导连续不是一个东西。
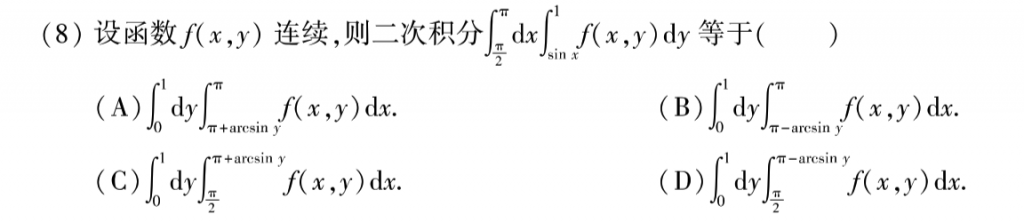
这题比较麻烦的是那个$arcsin$的定义域实际上只有$(-\frac{\pi}{2}, \frac{\pi}{2})$,所以要用一手诱导公式,具体的过程如果不会的话建议哔哩哔哩搜一下考研数学arcsinx

第九题也是想当经典的题,先用分块矩阵的乘法(矩阵分解)的方法,写成$(\alpha_1, \alpha_2, \alpha_3) \times matrix$的形式,matrix表示一个矩阵,然后用一手$R(AB)=R(B)$,(前提是A可逆),然后就好了。
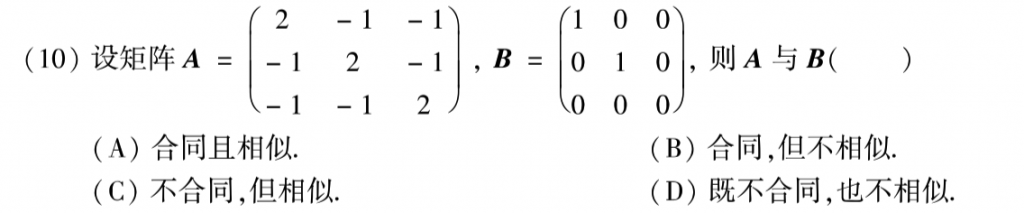
直接看迹就发现相似寄了,然后因为A和B都是实对称矩阵,看看他们的正负惯性指数是否相等,然后就可以推出来它们是合同的了。
这里补充一下求A的特征值的快速方法,A可以写成:
$$A=\begin{bmatrix}
-1& -1 &-1 \\
-1& -1 &-1\\
-1& -1 &-1\\
\end{bmatrix} +
3E$$
然后前面那个是秩一矩阵,特征值是-3, 0, 0(常用结论),然后再加3,A的特征值就出来了,是不是很神奇?

基础题
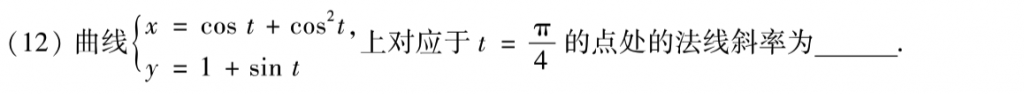
基础题
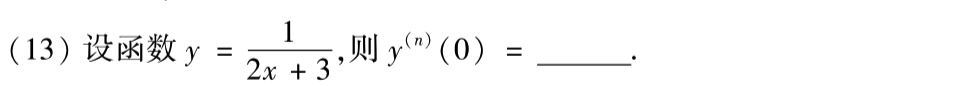
这题也不难,但是我写错了。。要细心!
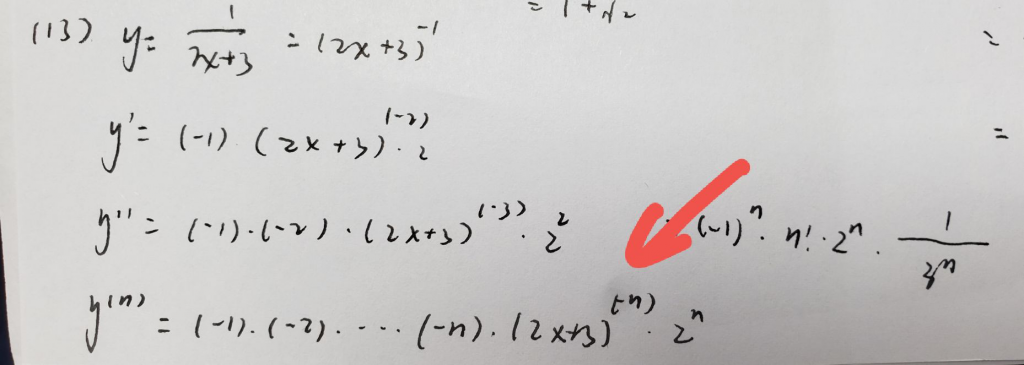
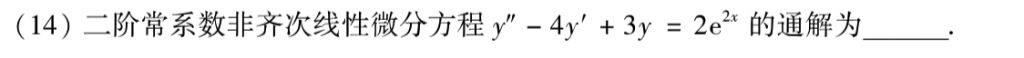
这题也是基础中的基础
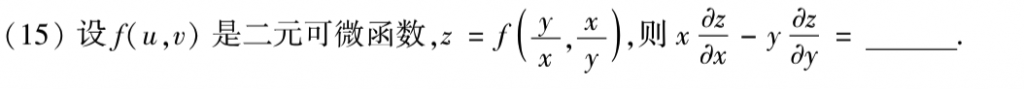
基础题,直接求导就好了

这种题有一个结论,永乐大帝的强化课也讲过,就是这种有一个斜线全是1的,而且是在主对角线上面的,每乘一次,这些1就会往上移动一格。

这题我感觉我的细节有些问题,没有答案写的那么清晰,主要是推$f(0)=0$的时候,还是要写的稍微详细一些。

第二问没截上来,懒得截了,也不难,就是计算有些麻烦,各种凑微分的时候要补充的系数,要慢一点理清楚

这题我给搞复杂了,实际上直接降阶,然后把x当成函数就好了,我的方法是左右两边乘了$y'$,然后前面那个$y'y''=\frac{1}{2}(y'^2)'$,然后换元$u=y'^2$,写完之后还自豪了一会,这么难的题都想出来了,实际是自己想复杂了。。。

基础题

这题我思路就错了,首先这道题的辅助函数很简单,直接$F(x)=f(x)-g(x)$就好了,然后分类,是否在同一点取得最大值,如果在同一点,那就简单了,三个点相等,反复罗尔就好。问题就在于如果最大值不在同一点,我想了不少方法,拉格朗日、泰勒啥的,凑了半天。。然后还没搞出来,就放弃了,硬是没想到零点定理这个东西。。。或者反证的手法也很漂亮。
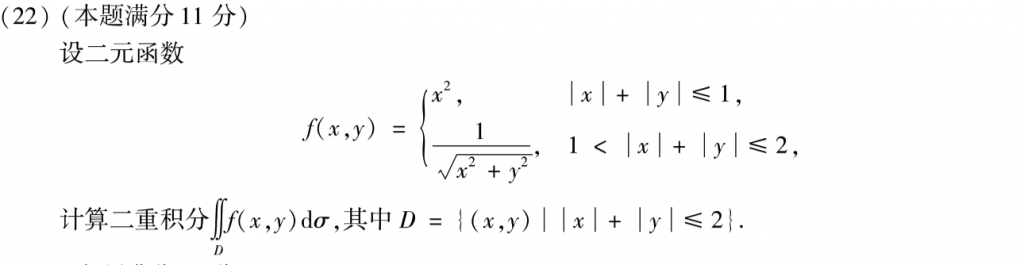
难度不大,主要是计算那个\(\int \frac{1}{sin\theta + cos\theta}d\theta\)要稍微细心一些(定积分带值的时候)

实际上就是这两个方程拼起来有解,就化简、分情况就好了,不难。

这题第一问也不难,主要第二问计算的时候,实际上很多人都是用相似对角,计算量大,不好,求逆矩阵还容易算错,用李正元全书上的方法就会简单很多,我来简要描述下这个方法:
首先是如果要求AX=B,是可以用初等行变换来算的,$(A, B)\to(E, X)$(对A进行初等行变换,对B也进行同样的操作,然后最后A变成E的时候,B就变成X了)
比如对于一个一般的矩阵来说,我们如果知道它的三个特征值以及对应的特征向量,那么就可以求A了,比如:
$$A(\alpha_1, \alpha_2, \alpha_3)=(A\alpha _1, A\alpha _2, A\alpha _3)=(\lambda_1\alpha _1, \lambda _2\alpha _2, \lambda _3\alpha _3)$$
两边取转置:
$$(\alpha_1, \alpha_2, \alpha_3)^TA^T=(\lambda_1\alpha _1, \lambda _2\alpha _2, \lambda _3\alpha _3) ^T$$
用上面那个算矩阵方程的方法,作初等行变换,就可以把$A^T$搞出来,然后最后A的话,取个转置就好了。
复盘结束,感谢阅读,码字较快,如果有什么问题,欢迎在评论区留言!







Comments NOTHING