这套卷子是今天上午写的,一个半小时不到就做完了,居然粗心错了一个选择题,太不应该了。
做了几张超越再做真题感觉就降维打击,下面开始复盘

第一题就比较基础,趋向无穷的时候sin和cos都是震荡的,所以只用看一次项系数就好了
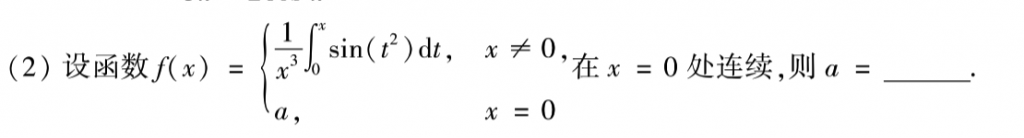
基础,考察连续的概念

这道题可以直接凑,也可以用三角换元,基础

把右边移到左边就是一阶线性其次,带公式就好了
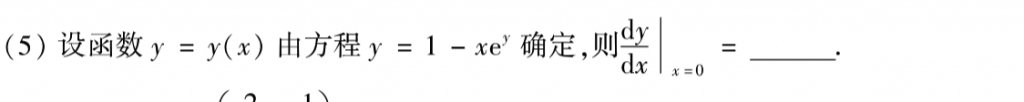
这题我大意做错了。。。下面是我的草稿纸:
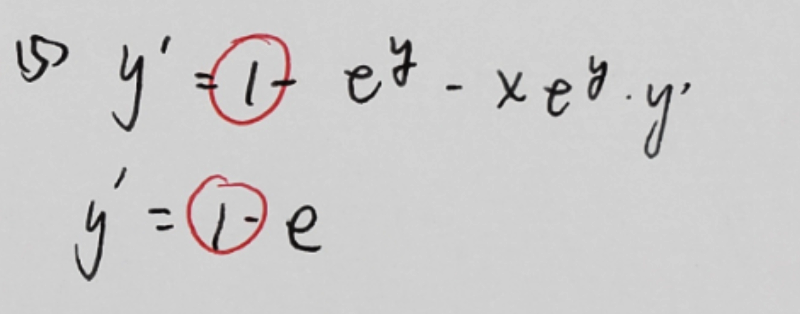

也是基本题,把右边的B移动到左边,然后提公因式啥的,再取行列式计算就好了。
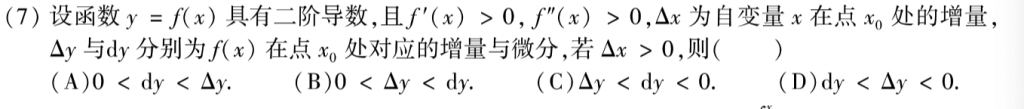
画一个递增的凹曲线,然后作一个切线,dy是切线的改变量,$\Delta y$是曲线的改变量,然后观察就可以得到结果了。

$f(x)$是奇函数,那么$F(x)$就是偶函数,然后$f(x)$是可积的,则$F(x)$连续,这是一个基础结论,另一句话是$f(x)$连续,$F(x)$可导。
这里再来复习一下可积性定理和原函数的存在定理,实际上这两个定理并没有什么联系,是两个独立的东西。
- 可积性定理:
- 如果$f(x)$在闭区间上连续,那么可积(可积也就是定积分存在)
- 如果$f(x)$在闭区间上有界+有限间断点,那么可积
- 如果$f(x)$在闭区间上存在有限个第一类间断点,那么可积
- 如果知道$f(x)$可积,那么可以推出$f(x)$有界,其他的东西推不出来嗷
- 原函数存在定理:
- 如果$f(x)$连续,那么一定存在原函数
- 如果$f(x)$有第一类间断点,那么一定不存在原函数
- 如果$f(x)$有第二类间断点,则需要具体问题具体分析
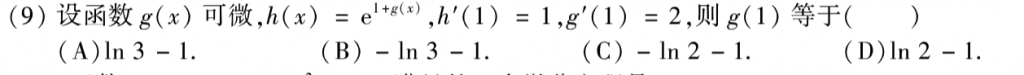
第九题也是送分题,求个导往里带值就出来了

先根据通解的结构,把齐次方程弄出来,再把$xe^x$往齐次方程里头带,就可以得到非齐次项
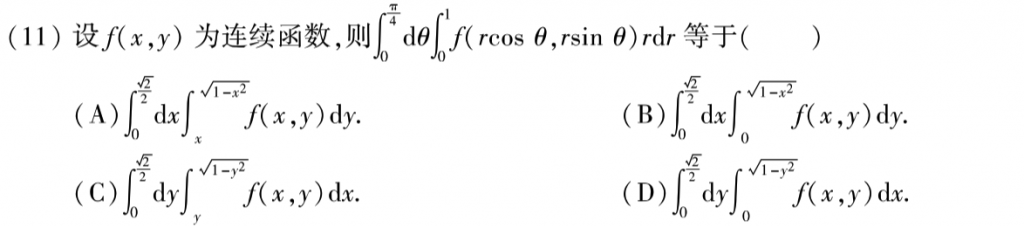
基础题,图画出来就ok了
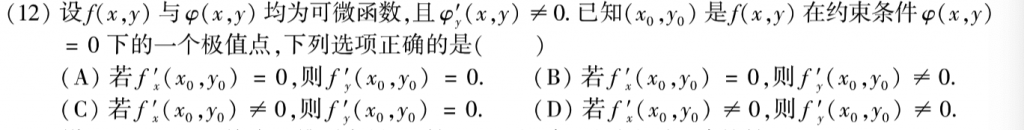
这个题还是有点难度的,我想了一会才想出来,首先题目关键词约束条件+极值点,那么肯定就要想构造拉格朗日方程组了,构造完成以后,最重要的一步就是把第二个方程的$\lambda$弄出来,带到第一个方程里面去,然后根据选项来分析。

基础题$R(AB) \le R(A)$就出来了

把初等变换的矩阵写出来就好了。
这里复习一下初等矩阵和它的逆矩阵之间的关系,如果是这种倍加的,那么逆矩阵就是负数,如果是交换某行某列的,那么逆矩阵就是本身,如果是倍乘的,那么逆矩阵就是对应位置的倒数。
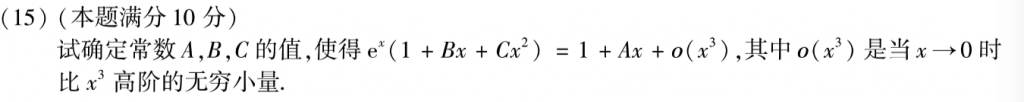
把$e^x$麦克劳林展开,然后对比系数

我一般见到不定积分中有$e^x$,而且有些眼花缭乱的,就会想到作变量代换$e^x=t$,然后再算就方便了。
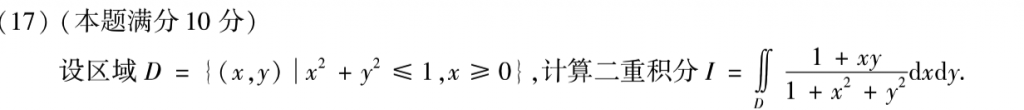
这题也简单,主要是要注意奇偶性的使用

超级简单的单调有界题目,有界直接归纳法就可以了,单调的话用一下那个$sinx \le x$的不等式,如果实在记不住可以听一听王谱老师的弦切定理,传送门:https://www.bilibili.com/video/BV1wg4y187fh/
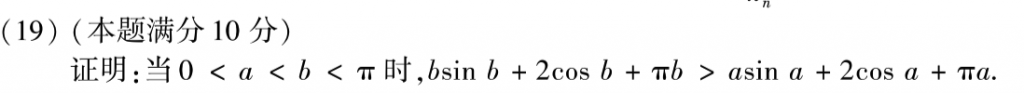
构造函数求导,判断单调性,基础中的基础

这题很多地方都有,660,辅导讲义上的,主要是求导的时候要有耐心和要细心,不然很容易出错,中途一旦某一步错了,最后结果对不上就会挺慌的。

第一问凹凸性就直接求二阶导,然后第二问就是中学的几何知识,李正元的全书上正好也有,基础不好的朋友可以看看,对应的例题和评注如下:

第三问也不难,直接用三角形的面积减去那个曲线与x轴围成的面积就挺简单
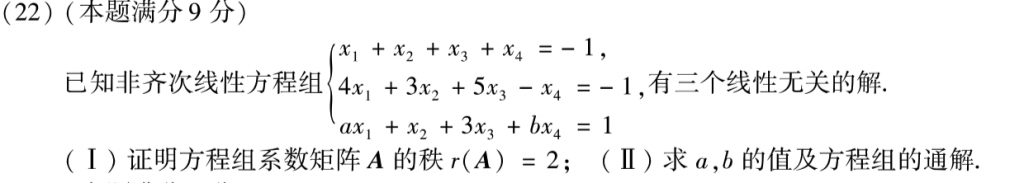
第一问这个其实有个结论,就是$Ax=b$的线性无关的解的个数为$n-r(A)+1$。
第二问啥的就基础了。

每行之和均为3就给了特征值和特征向量,然后第二问就正交化单位化后拼成Q就好了,要注意的是特征值和特征向量的对应。
复盘结束,感谢花时间阅读,码字较快,若有问题请在评论区留言!







Comments NOTHING