昨天上午做了13年的第三套,也是13年的最后一套,本来打算晚上总结的,结果天气好,打了一下午+一晚上的篮球羽毛球,总结自然也就搁置了,今天来总结一下。
客观评价这张卷子,我感觉难度和第二套差不多,总体难度是非常大的,考了很多很细的概念,证明题也比较刁钻,不过这套试卷的计算量比较友好。
现在开始复盘。

第一题这种函数我称之为动态函数,要先根据x的取值不同来确定函数,然后判断间断点,然而这道题我做错了,我直接把0和2往里头带,感觉是两个无穷是选了B,结果挖了坑...还是要先把函数解析式求出来,然后再具体分析。

这道概念题出的很棒,可以趁这道题复习一下\(f(x)\)和\(|f(x)|\)它们之间连续的关系、可导的关系以及可积的关系。
- 如果\(f(x)\)连续,那么\(|f(x)|\)是连续的,但是反之不能推,比如$x$小于零的时候\(f(x)=-1\),$x$大于零的时候\(f(x)=1\)这个例子就可以反证了。
- 如果\(f(x)\)在$x=a$处可导,那么对于$|f(x)|$:
- 如果\(f(a) \ne 0\),那么$|f(x)|$在a处是可导的,画图就很清楚了。
- 如果$f(a)=0$,那么就要继续分情况,如果是和$x$轴相切,那么$|f(x)|$在$a$处也是可导的。但如果穿过了$x$轴,那么就不可导了。(图像图像)
- $|f(x)|$的导数推$f(x)$就是这道题的D
- 如果$f(x)$可积,那么$|f(x)|$可积,反之不能推,例子就是狄利克雷函数

直接把1带进去,然后看$f'''(x)$,看不出啥,继续求导,直到五阶导不等于零,这个时候就能推拐点了,武忠祥强化课讲过这玩意。

基本题,pass
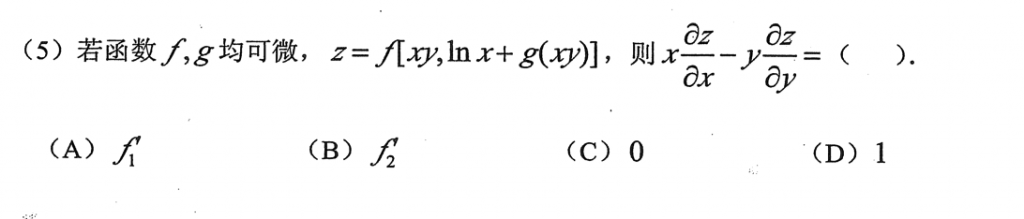
基本题,pass
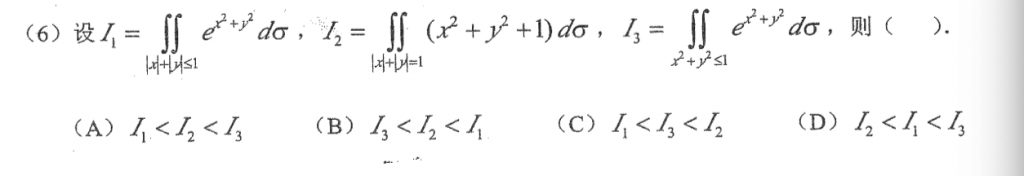
拿\(I_1\)当中介,被积函数大的就大,积分区域大的就大
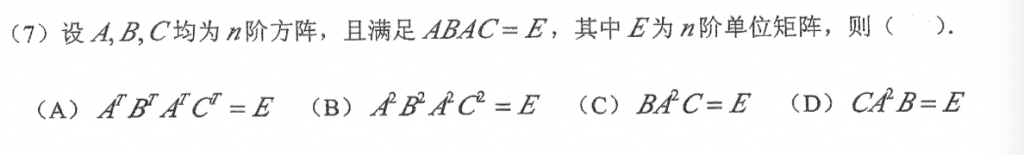
这道题我做错了,是相当好的一道题,$ABAC=E$可以推\(C^{-1}=ABA\),然后带入\((CC^{-1})^{T}\)就出来了,感觉还是不容易想的。

这道题是好题,李艳芳讲了这个东西,https://www.bilibili.com/video/BV11r4y1Q7iC/?spm_id_from=333.337.search-card.all.click 第三集的十分钟左右
先把二次型对应的矩阵改造成对称矩阵,就是加上它的转置,然后除以二就好了,可以证明这个矩阵的秩是等于二的(夹逼,小于2用$R(AB)<=R(A)+R(B)$,大于2用证明存在二阶子式不等零),然后就可以推出一定有零这个特征值,然后CD就证明了,B我还不会证明,等一个大佬在评论区补充hh
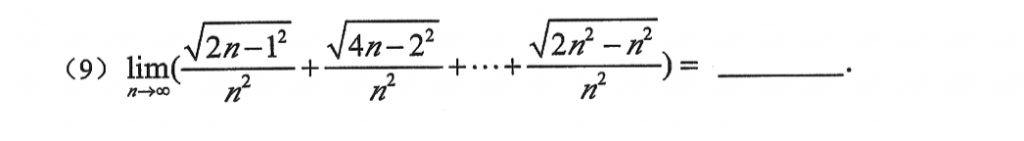
这题就很明显的定积分定义了,提可爱因子到前面,然后对后面这玩意变形,配方啥的,要多尝试。

换元分部积分啥的,就出来了

这题就是把$y$当成自变量,然后$x$当成$y$的函数就好了
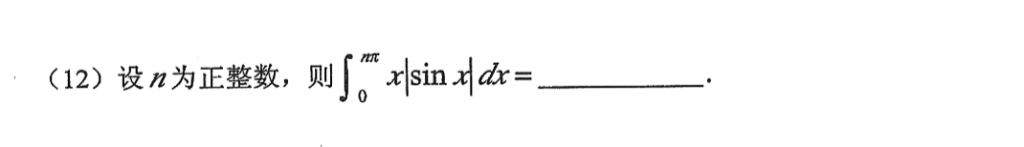
这题答案的方法我看的云里雾里的,不如直接用区间再现,先令\(x=n\pi-t\),具体过程看图:
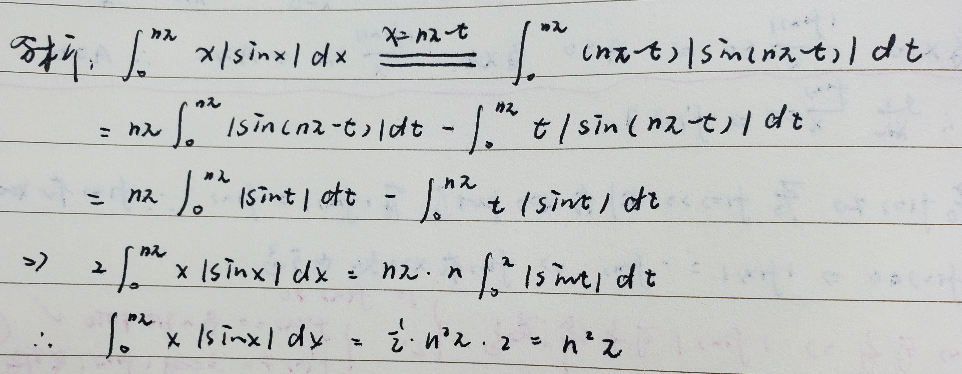
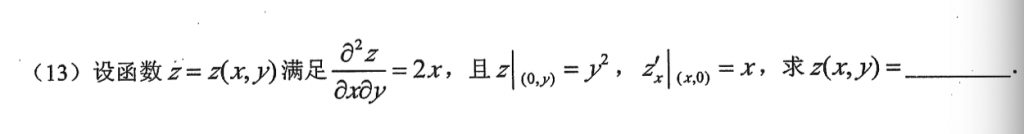
偏积分就好了,不难。

根据后面的那个矩阵方程可以得到两个特征值,然后再根据迹,可以求出第三个特征值,行列式就出来了。
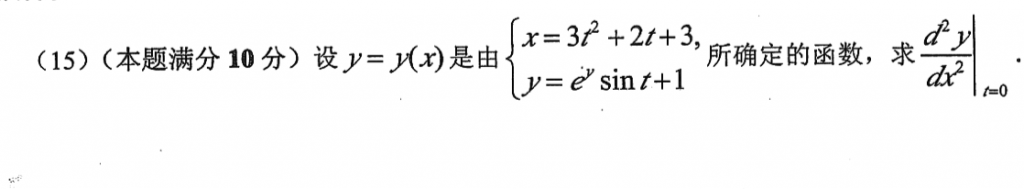
其实像这种隐函数啥的杂糅的参数方程的二阶导,我觉得快一点的方法就是先单独计算\(x'(0), y'(0), x''(0), y''(0)\),然后再用公式:\(\frac{x''(0)y'(0)-y''(0)x'(0)}{x'^{3}(0)}\)就比较快了,这个公式记忆也挺简单的,就是要记住分母是三次方就ok
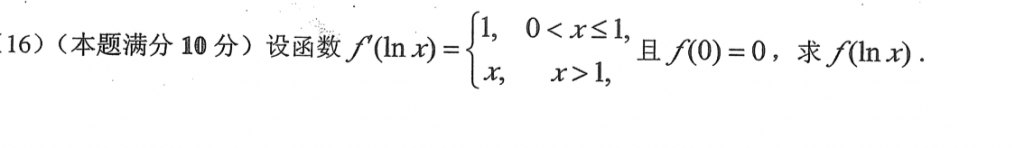
这道题也不难,先换元,搞成$f'(x)$的形式,然后再积分,然后再把$lnx$带进去就好了

这道题又是我思维定势的体现,第一问就不说了,题目给了个函数方程,因为我之前做过不少函数方程的题,使用的方法都是用导数定义,然后得到一个微分方程,再求解,正好看到第三问就是求$f(x)$,所以一直在往这个方向试,试了半天没试出来就放弃了。。。结果发现就是对式子直接求导,然后换元就出来了。。第三问也是,直接把$y=1$就能把微分方程搞出来了,厉害👍

这道题好像也和22那道挺像的,结果我又给算错了!主要就是这个积分算错了:\(\int_{0}^{\frac{\pi}{4} }\frac{cos\theta -sin\theta }{(sin\theta +cos\theta )^2}dx\),没意识到分子直接凑进去就是分母,还是不够敏感。。也可能是好久没铺天盖地的刷不定积分了,手生了。

这道题我就感觉做过好多遍,严选题上好像就有,不难,就是放缩,然后牛顿莱布尼兹公式凑啥的,慢慢试就可以试出来,不能急,第二问就单调有界

这道题也是基本题,计算一定要细心!
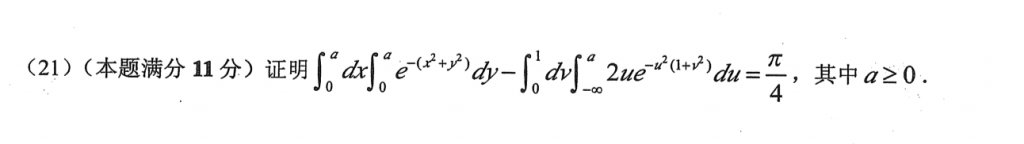
我拿到这道题就在想构造一个关于a的函数,然后求导证明方程是一个常数方程,结果对二重积分的变限积分求导模糊了,搞了半天,还没搞出来。。又发现一个弱点。
答案提供了两个思路,第一个思路就是直接计算,两个不能算的积分可以抵消掉,好手法!第二个思路就是我上面说的证明函数是常数方程。

这道题感觉也不难,第一问基本就是白给,第二问因为正交就可以推出后面那个转置的矩阵乘B等于零了,所以\(\beta\)是零的特征向量,然后第一问说了可以唯一线性表示,就用定义写开;\(\gamma=k_1\alpha_1+k_2\alpha _2+k_3\alpha _3\),然后和A相乘就好了。

第二十三题也是非常简单的题,但是引发了我的一个思考,因为我在做这道题的时候,通解是自己找的,并没有用它给的\(\xi _1,\xi_2\),因为我怕特解可以被通解线性表示,主要是也没想清楚,复盘的时候发现担心是多余的。
假设\(Ax_1=0, Ax_2=b, b\ne 0\)
第一种情况,如果A是满秩的,那么\(Ax_1=0\)只有零解,\(Ax_2=b\)有唯一解,此时它们俩肯定是相关的,因为零向量和任何向量都相关嘛,但是这并不是本题的情况。
第二种情况,如果A不满秩,那么肯定其次方程肯定有非零解,如果此时\(x_1 \ne 0\),然后用定义:\(k_1x_1+k_2x_2=0\),两边乘A,就可以推出他们俩是无关的了,也就是本题的条件。
而如果\(x_1 = 0\),那他们肯定就相关,这也不是本题的条件。
所以我的担心其实是多余的,直接根据那俩特解把通解写出来就好了。







Comments NOTHING