前面我们介绍了如何对数据进行处理以及常见模型的形式,中篇太过于理论,在实际的建模中,我们可以用SPSS非常方便快速的估计出模型,我们只需要好好分析即可。
SPSS专家建模器思路:
- 处理数据的缺失值问题、生成时间变量并画出时间序列图
- 数据是否为季度数据或者月份数据(至少有两个完整的周期,即两年),如 果是的话则要观察图形中是否存在季节性波动。
- 根据时间序列图大致判断数据是否为平稳序列(数据围绕着均值上下波动, 无趋势和季节性)
- 打开SPSS,分析‐‐时间序列预测—创建传统模型,看看 Spss专家建模器得出的优的模型类型。
- 如果后的结果是ARIMA(p,0,q)模型,那么我们就可以画出时间序列的样本 ACF和PACF图形进行分析;如果得到的是ARIMA(p,1,q)模型,我们可以先对数据进行 1阶差分后再用ACF和PACF图形分析;如果得到的结果与季节性相关,那么我们可以考虑使用时间序列分解
例题:根据某产品2014‐2018年季度销售数据,预测未来两年的销售数据。
也就是我们在第一篇文章中用到的数据集,首先还是创建时间变量和观察时序图
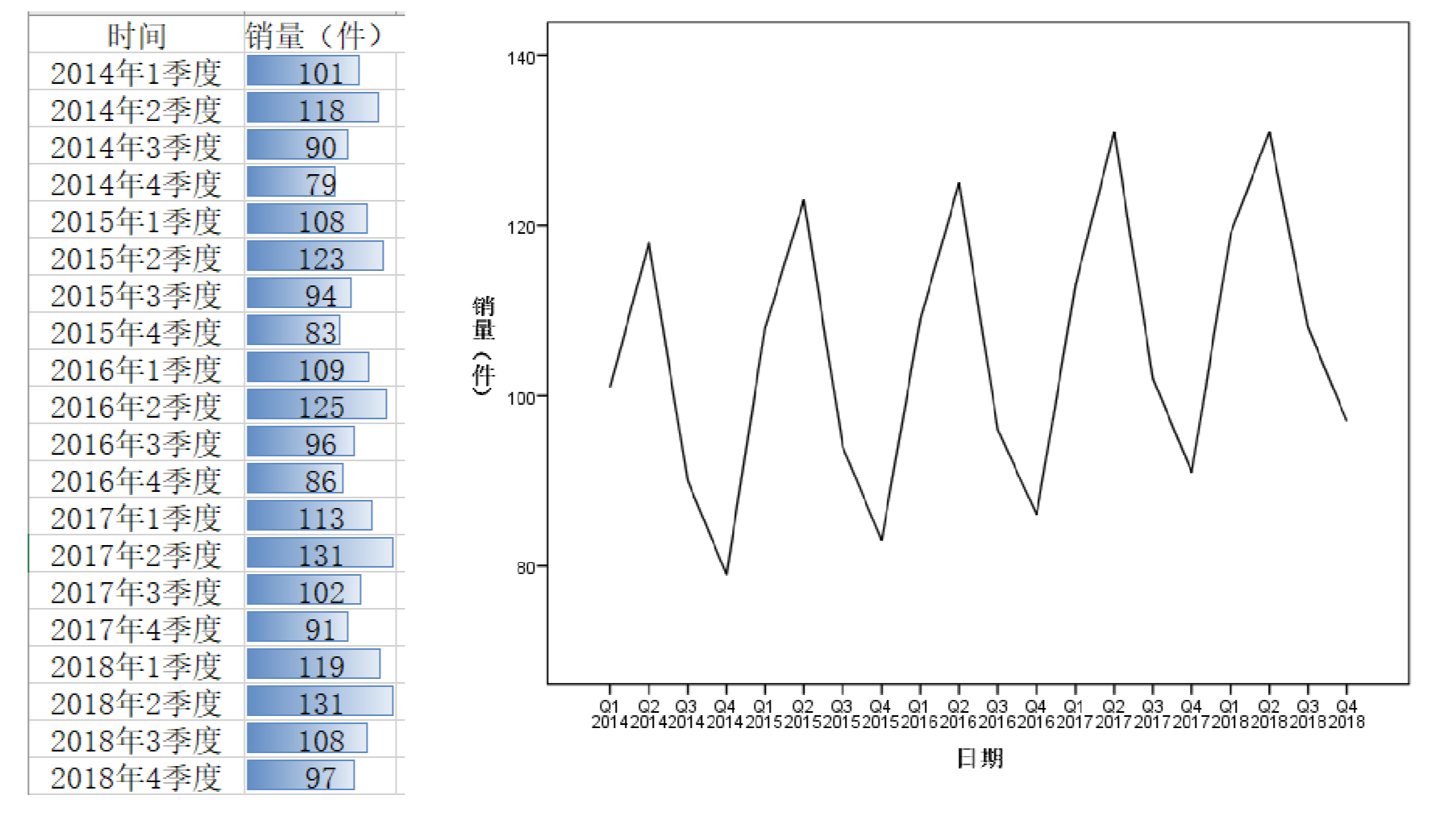
然后使用专家建模器看看它给我们选的是什么模型:
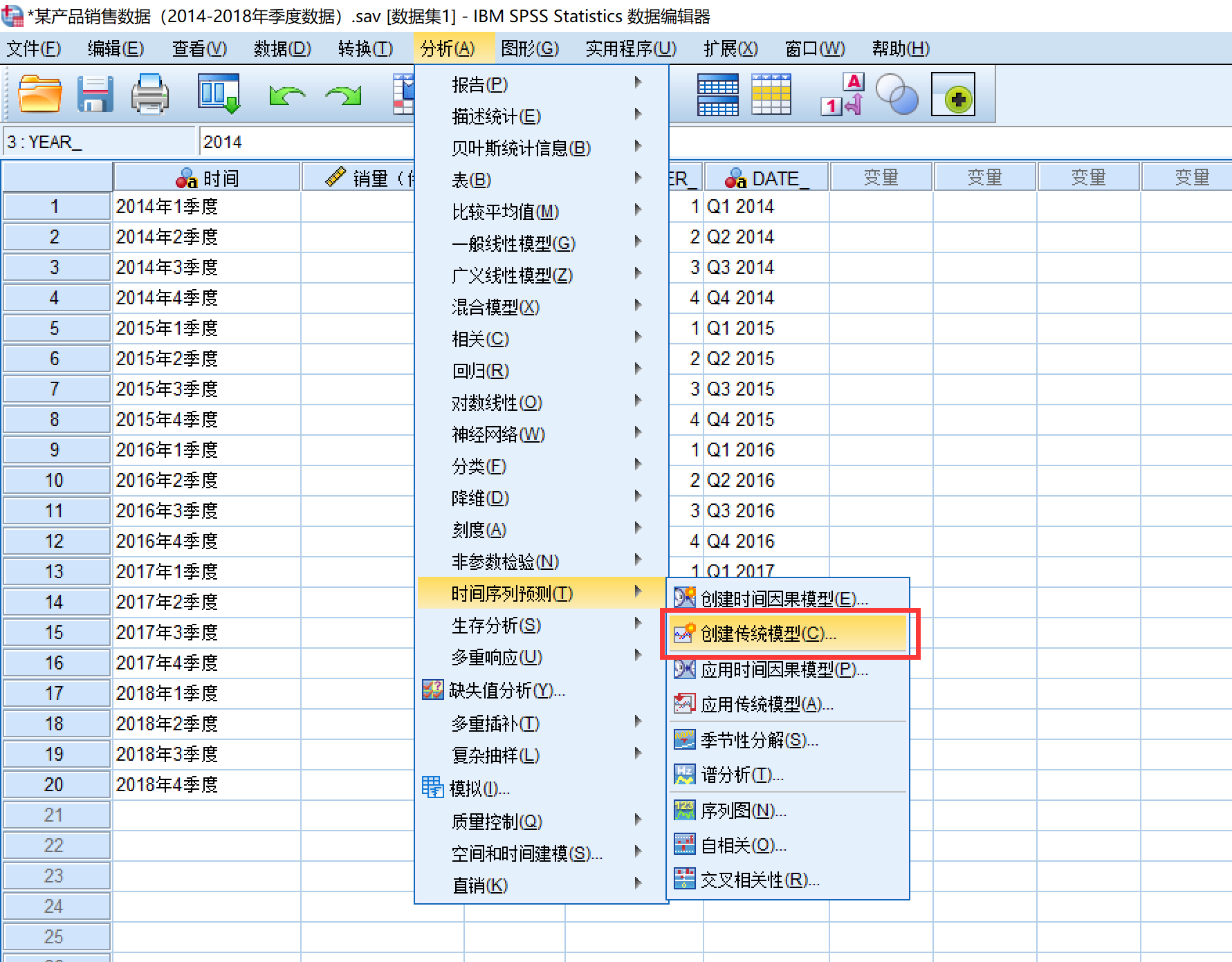
将销量加入因变量后,什么都不用管,直接点确定
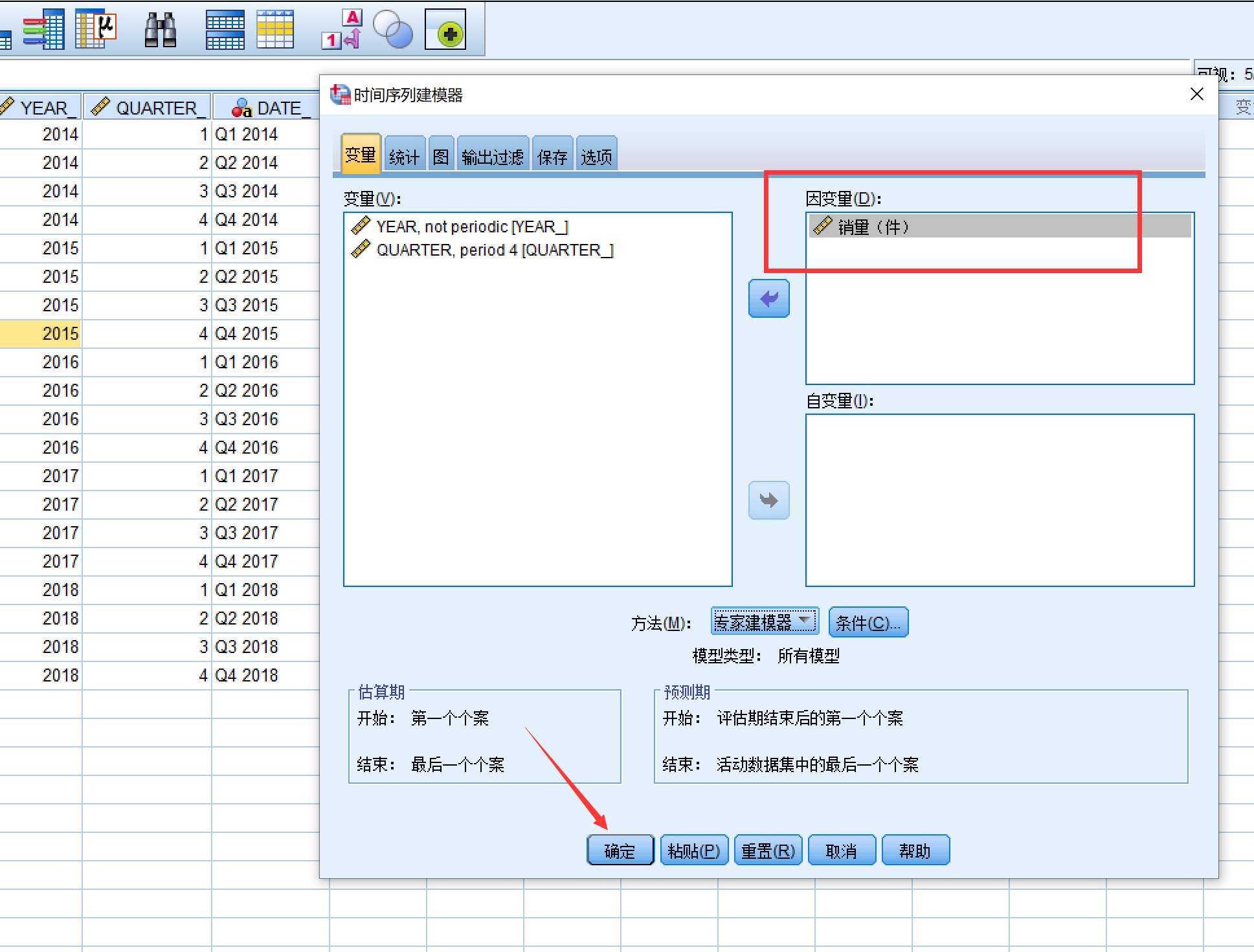
然后spss就给我们找到了最合适的模型:温特加法模型:

所以,我们下面的思考都以这个模型为基础:
- 数据为季度数据(有四个周期),从时序图中看出也有季节性波动,即第二季度的销量较高, 第四季度较低;
- 根据时间序列图可知数据不平稳,有向上的趋势
- Spss的专家建模给出的合适的模型是温特加法模型
- 温特加法模型意味着原时间序列数据含有线性趋势和稳定的季节成分,我们可以使用加法时间序列分解,看一下数据的特征,用完之后,再用温特加法预测
- 利用Spss我们可以对未来两年的销售数据进行预测。
前面的简单分析搞完之后,我们来看看正式的操作步骤,还是点击创建传统模型:
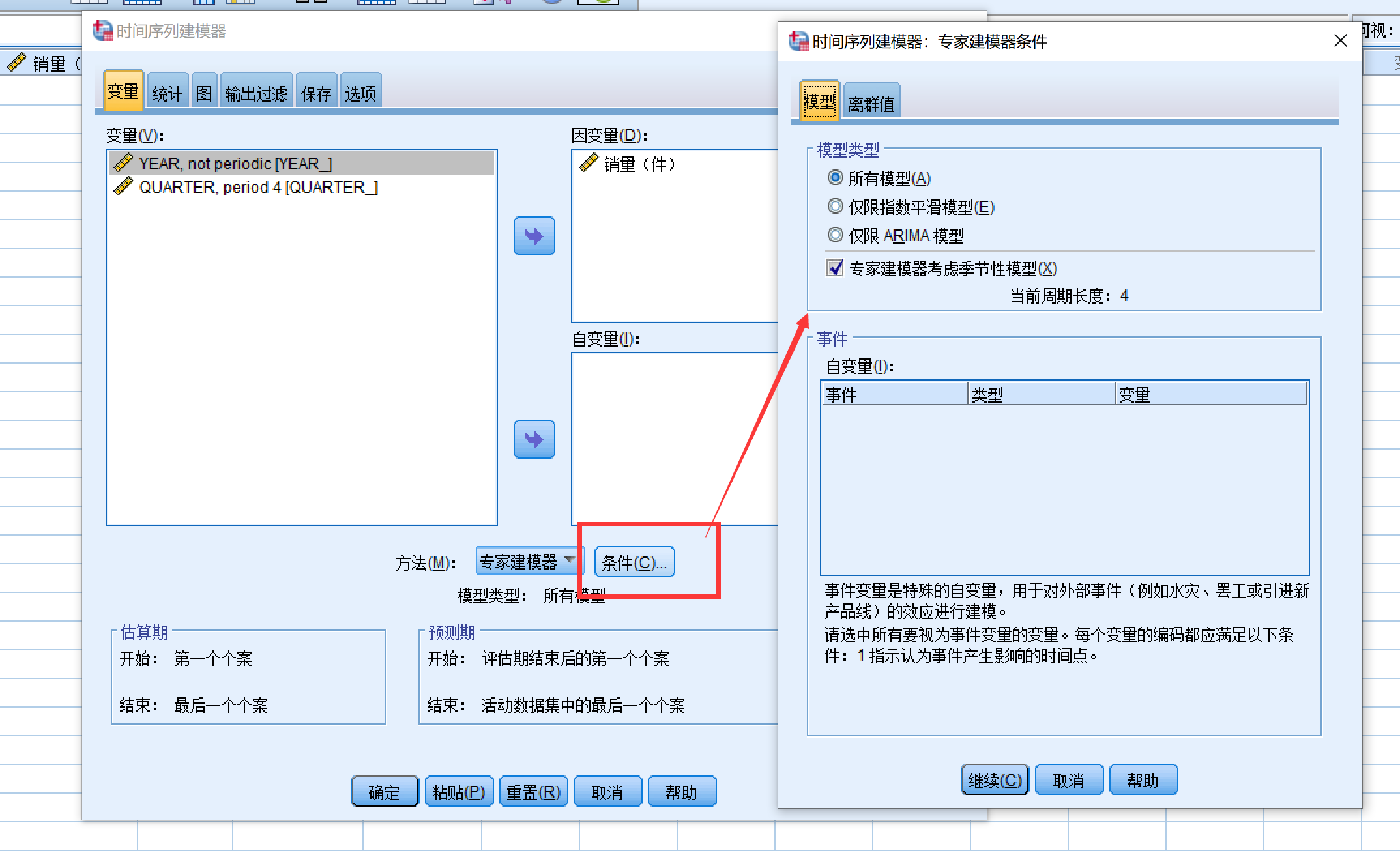
先点击条件,模型类型这里,最好是勾选上“所有模型”,当然,如果你只会分析指数平滑或者ARIMA,那就勾上其中的一个,“专家建模器考虑季节性模型”,这个选项一般来将,如果你的数据是有季节性的,那就勾上,如果没有,比如是年份数据,那就没必要勾。
然后点击右边的离群值,这里就是spss自动帮我们检测异常值,将他们都勾选上,spss会对发现的异常值使用序列平均值来代替。
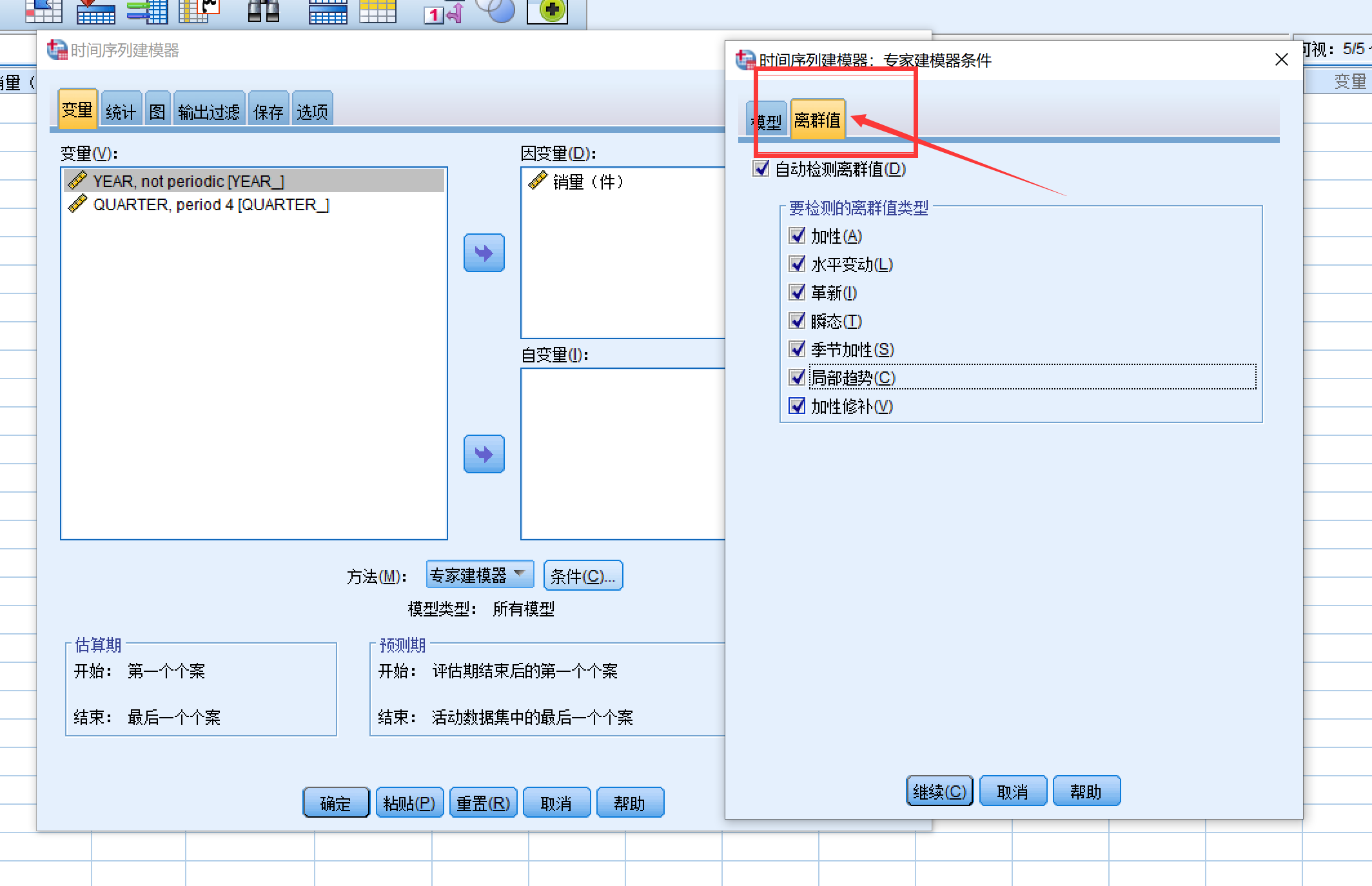
点击继续之后,找到统计选项,这里需要勾选上参数估计值,这样的话SPSS才会将模型估计到的参数汇报给我们,否则是不会汇报的。
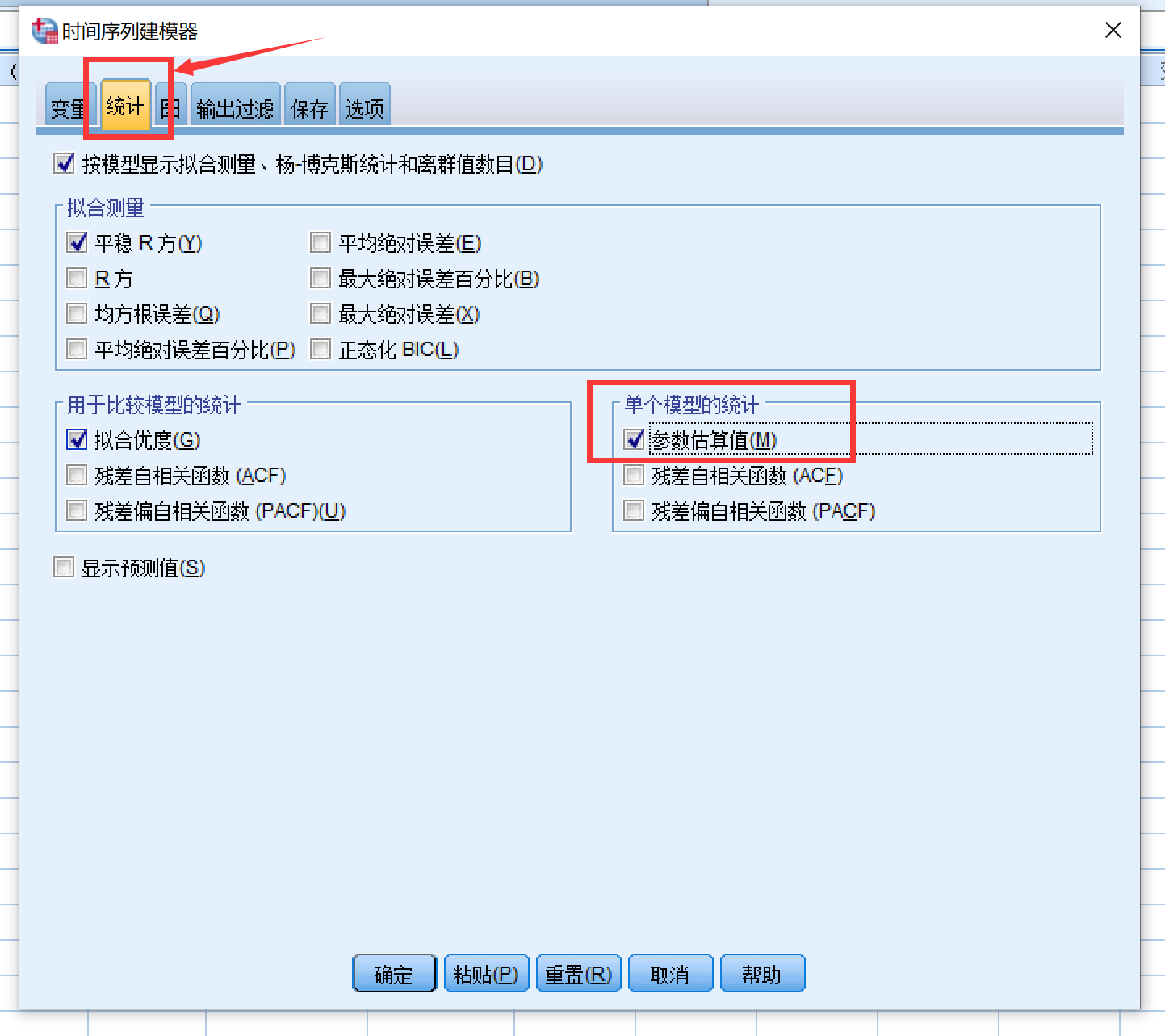
然后点击旁边的“图”选项:这里需要勾选上拟合值,预测值和拟合值是不同的,预测值是将样本外年份数据带入模型计算得到的结果,而拟合值是将样本年份重新带入模型计算得到的,而ACF和PACF可以帮助我们判断残差是否为白噪声,即改时间序列是否能被完全识别。
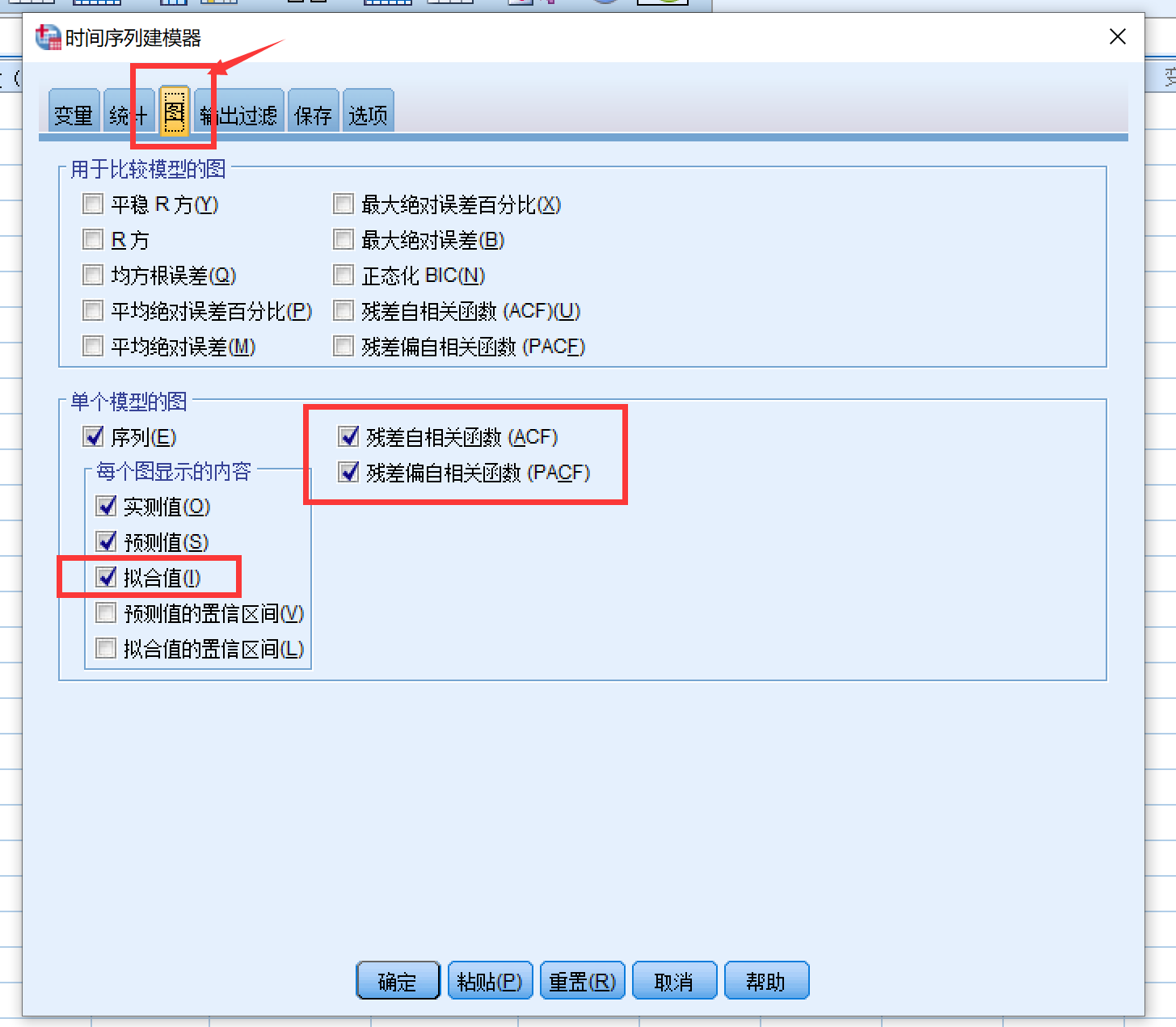
然后输出过滤不用管,点击“保存”,然后勾上预测值:
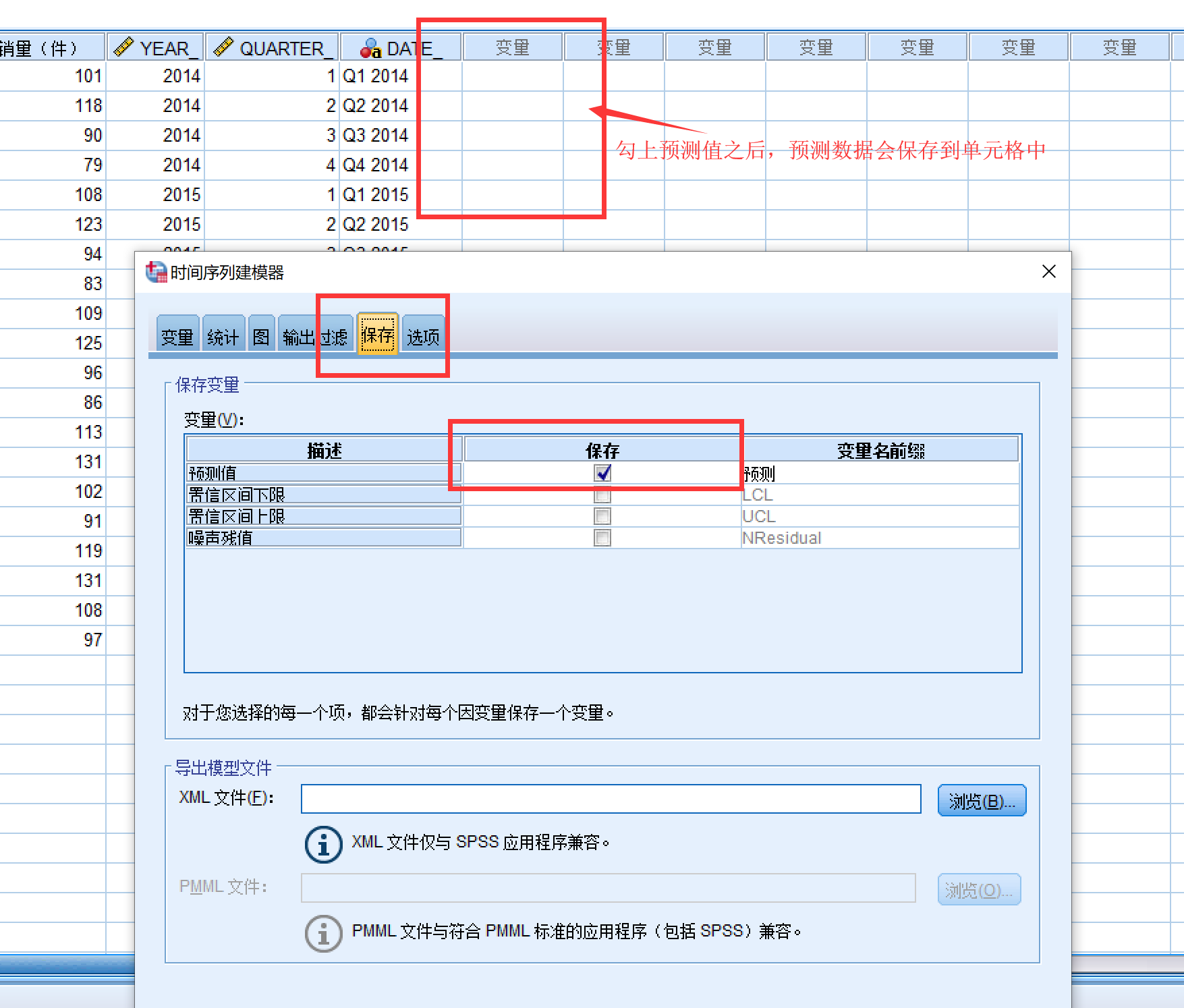
最后是“选项”,这一步非常重要,选好了之后spss才会帮我们预测:

都填完了之后,就点击确定,然后spss就开始工作了。
评价模型好坏
如何评价模型的好坏,spss给了我们一些参数,其中最重要的是平稳的R方和BIC准则,这两个指标既考虑了拟合的好坏,又考虑了模型的复杂度,R方可以用来反映线性模型拟合的好坏,越接近于1越准确
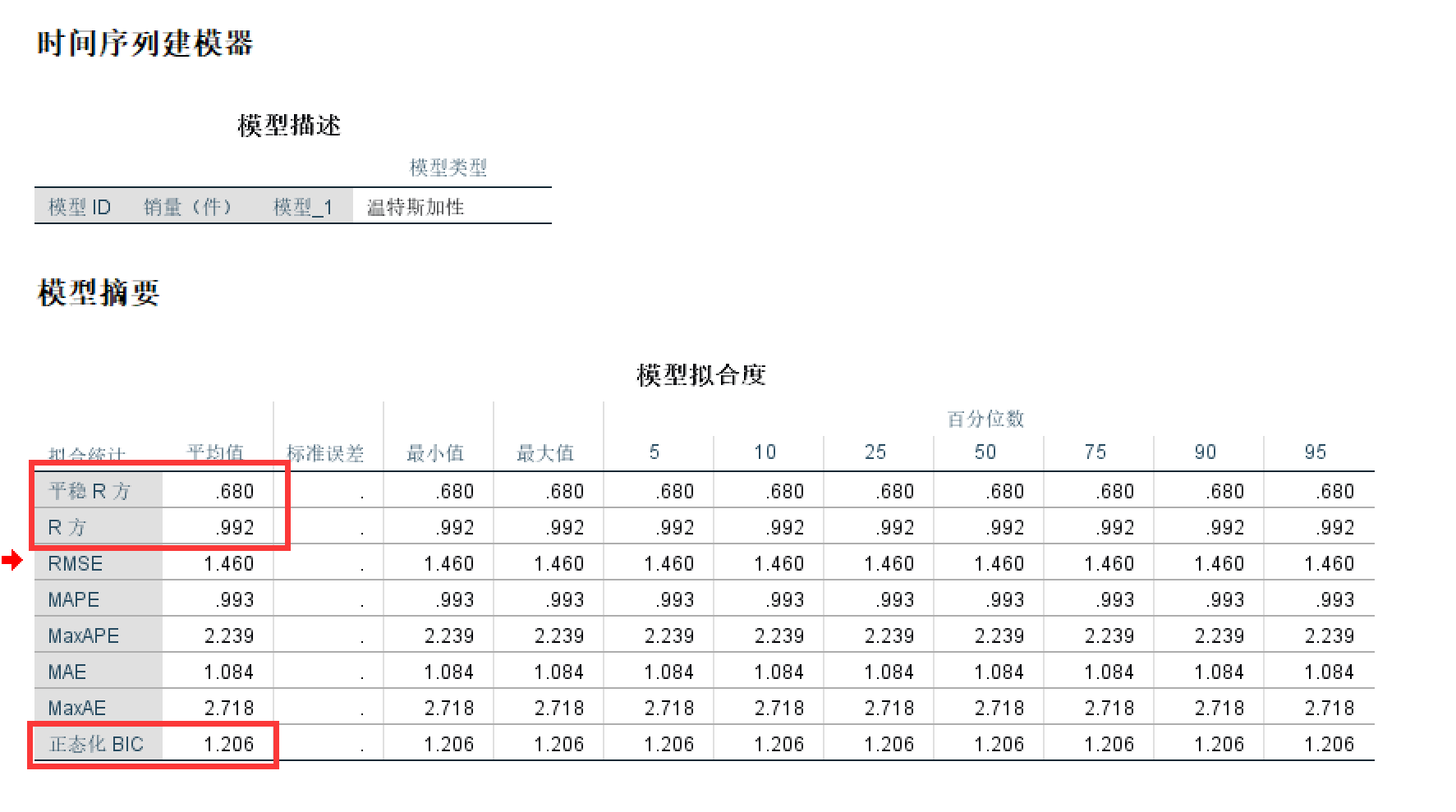
在这道例题中,R方高达0.992,可以说是很恐怖了,平稳R方也接近0.7,BIC是一个相对量,一般用于模型之间的比较,两个模型,谁的BIC越小谁就牛逼,一般来讲的话BIC越接近于0越好。
参数估计值
首先我们知道温特加法模型如下:
$$
\begin{cases}
l_t=\alpha \left( x_t-s_{t-m} \right) +\left( 1-\alpha \right) \left( l_{t-1}+b_{t-1} \right)\\
b_t=\beta \left( l_t-l_{t-1} \right) +\left( 1-\beta \right) b_{t-1}\\
s_t=\gamma \left( x_t-l_{t-1}-b_{t-1} \right) +\left( 1-\gamma \right) s_{t-m}\\
\hat{x}_{t+h}=l_t+hb_t+s_{t+h-m\left( k+1 \right)}, k=\left[ \frac{h-1}{m} \right]\\
\end{cases}
$$
\(m\):周期长度,\(\alpha\):水平的平滑参数,\(\beta\):趋势平滑参数,\(\gamma\):季节的平滑参数,\(\hat{x}_{t+h}\):第\(h\)期的预测值
spss给我们的估计值(不要看表中的字母):
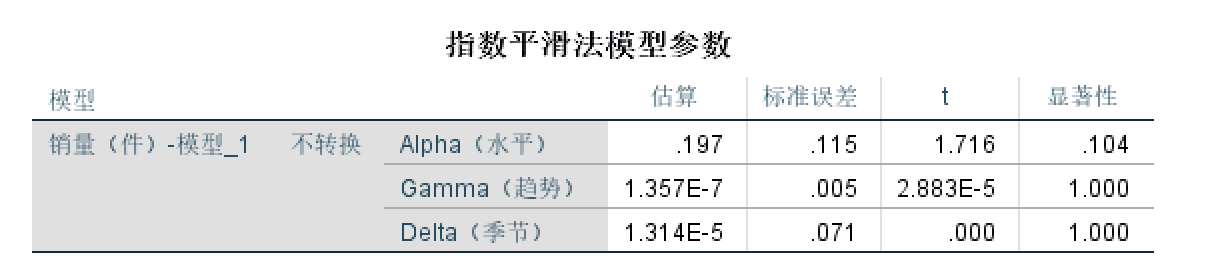
$$
\hat{\alpha}=0.197, \hat{\beta}=1.357\times 10^{-7}, \hat{\gamma}=1.314\times 10^{-5}
$$
白噪声进行残差检验
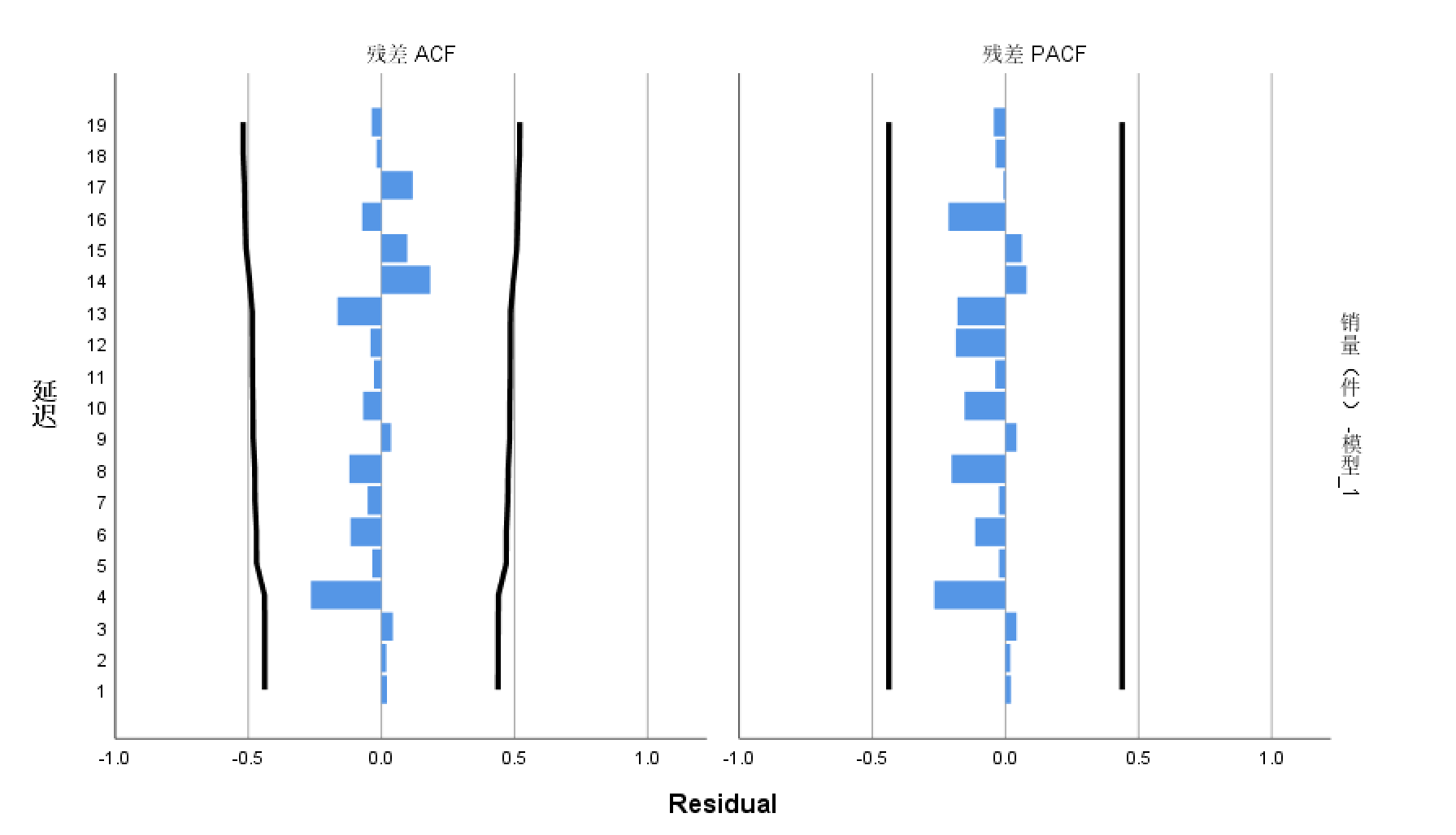
主要是分析ACF和PACF的图像:从残差的ACF和PACF图 形中可以看出,所有滞后阶数的自相关系数和偏自相关系数均和0没有显著的差异。(如果超过了0.5就说明有差异)
另外还需要分析Q检验的结果:(在中篇说了)
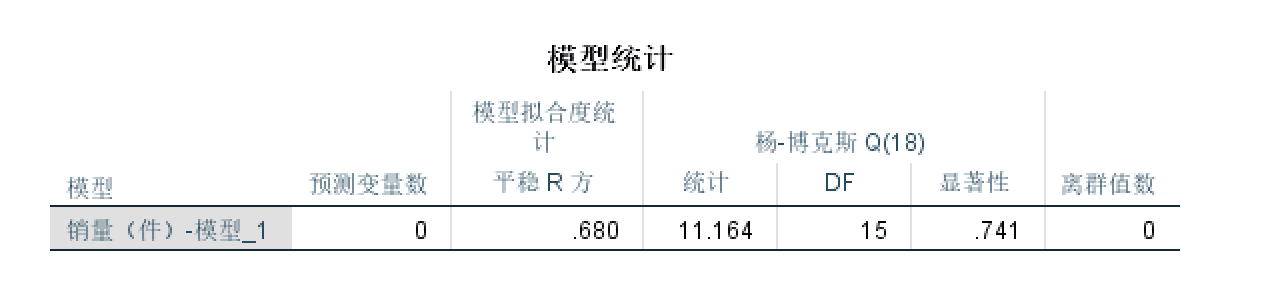
看这一列表格中的”显著性“这一栏,为0.741,我们无法拒绝原假设,认为残差就是白噪声序列,因此温特加法模型能够很好的识别本例中的销售数据。
预测结果和效果图
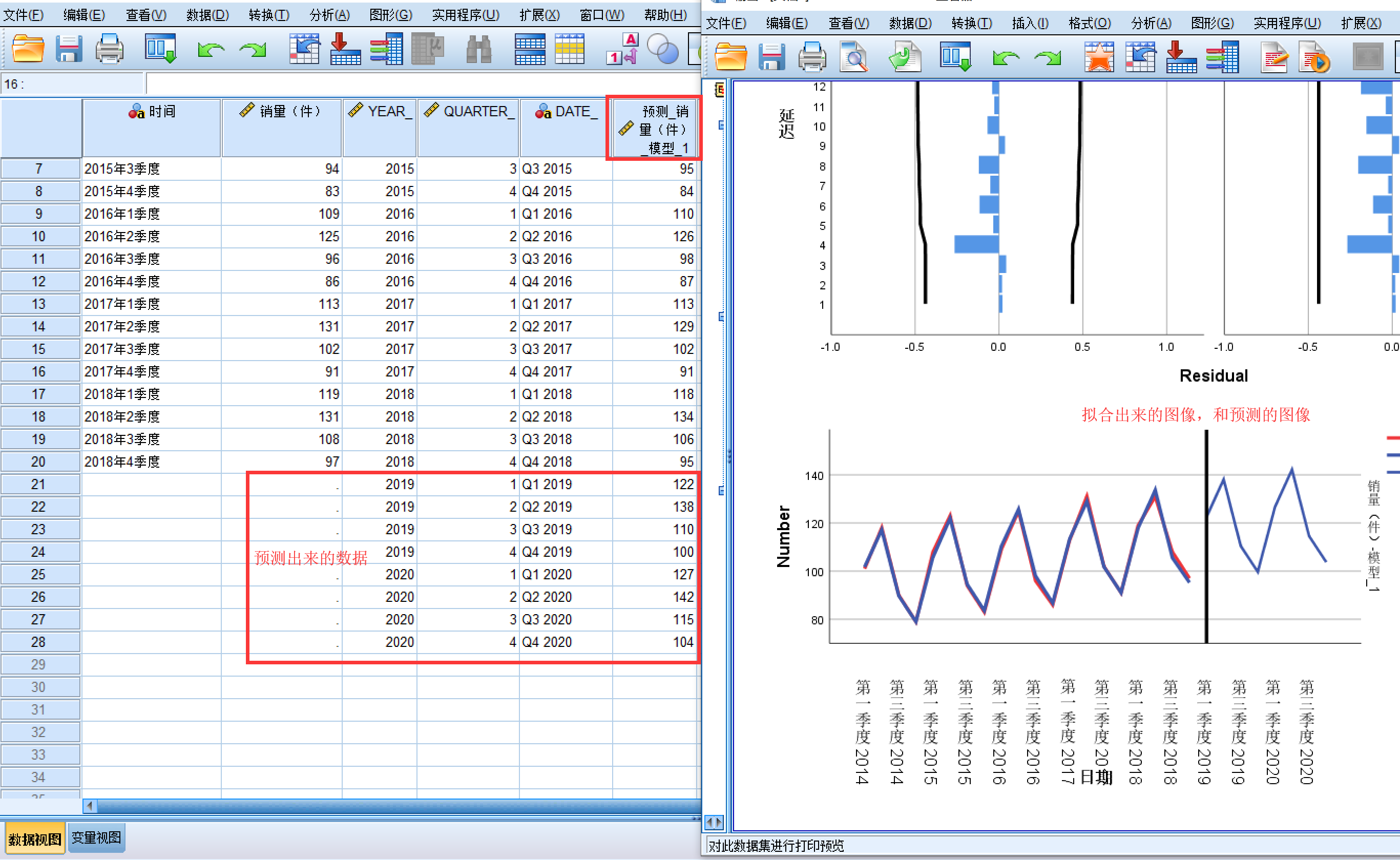
从图中可以看出,真实数据和拟合数据的时序图几乎重合,这说明温特加法模型对原数据拟合的效果很好; 另外,预测的后两年的数据既保留了原始序列的季节效应,也同时具有向上的线性趋势,这说明温特加法模型能很好的对该产品的销量数据进行预测。







Comments 1 条评论
我是菜鸡(markdown语法测试)