时间序列分析（中）——模型介绍

上一篇文章我们介绍了如何对数据预处理，以及使用基本的时间序列分解来进行预测，这一篇文章主要介绍SPSS中的专家建模器以及常见的时间序列模型。内容较难，了解一下即可...（重点在下一篇文章）

专家建模器

spss的官方文档描述如下：

翻译一下就是：

给我一个时间序列，我能自动帮你找到合适的拟合模型
我提供的模型有两类，一类是指数平滑模型，另一类是ARIMA模型
我可以自动帮你识别数据中的异常值

指数平滑模型

SPSS官方文档中的模型：

下面我们来逐一介绍，这些模型了解一下就好了，不用我们自己真正去计算，spss会帮我们计算好，我们只要将精力放在分析上就好了。

Simple模型

名称：简单指数平滑
适用条件：不含趋势和季节成分
与之类似的ARIMA：ARIMA(0, 1, 1)

令$x_t$为$t$时刻的观测数据，且令$S_t=\hat{x}_{t+1}$，即第$t+1$期的预测值，且满足$\hat{x}_{t+1}=\alpha x_t+\left( 1-\alpha \right) \hat{x}_t$，可以证明：

$$
\hat{x}_{t+1}=\alpha x_t+\alpha \left( 1-\alpha \right) x_{t-1}+\alpha \left( 1-\alpha \right) ^2x_{t-2}+\cdots +\alpha \left( 1-\alpha \right) ^{t-1}x_1+\left( 1-\alpha \right) ^tl_0
$$

也就是将公式展开，其中$l_0=\hat{x}_1$，也就是初始值，其中$\alpha$被称为平滑系数$\left( 0\le \alpha \le 1 \right)$，显然每个平滑后的数据都是由过去的数据加权后得到的，越接近当期的数据，其权重越大，这说明距离当期数据越近的数据，对当期影响越大，反之越小。

其中平滑系数$\alpha$的选取原则：

如果时间序列具有不规则的起伏变化，但长期趋势接近一个稳定的常数$\alpha$的值一般比较小，0.05~0.02
如果时间序列具有迅速明显的变化倾向，则$\alpha$应该取较大的值 0.3~0.5
如果时间序列变化缓慢，应该选择较小的值，0.1~0.4

实际上，这些工作spss都会帮我们做好，从公式可以看出来，简单指数平滑只能预测一期的数据，如果我们想预测后面的数据，可以将预测值加到样本里面去。

线性趋势模型

名称：霍特线性趋势模型
适用条件：线性趋势，不含季节成分
与之类似的ARIMA：ARIMA(0, 2, 2)

霍特在1957年把简单的指数平滑模型进行了延伸，能够预测包含趋势的数据，该方法包含一个预测方程和两个平滑方程（一个用于水平，另一个用于趋势）

$$
\begin{cases}
l_t=\alpha x_t+\left( 1-\alpha \right) \left( l_{t-1}+b_{t-1} \right)\\
b_t=\beta \left( l_t-l_{t-1} \right) +\left( 1-\beta \right) b_{t-1}\\
\hat{x}_{t+h}=l_t+hb_t, h=1, 2, \cdots\\
\end{cases}
$$

第一个方程称为水平平滑方程，第二个方程称为趋势平滑方程，第三个方程为预测方程

其中，$t$为当前期，$h$为预测超前期数，也称之为预测步长；$x_t$为第$t$期的实际观测值；$l_t$为时刻$t$的预估水平；$b_t$为时刻$t$的预测趋势，$\alpha$为水平平滑趋势；$\beta$为趋势的平滑参数。

阻尼线性趋势模型

名称：阻尼趋势模型
适用条件：线性趋势逐渐减弱且不含季节成分
与之类似的ARIMA模型：ARIMA(1, 1, 2)

经验表明：霍特的线性趋势模型倾向于对未来预测值过高，特别是对于长期预测，所以Gardner和Mckenzie在霍特的模型基础上引入了一种阻尼效应，用来缓解较高的线性趋势：

$$
\begin{cases}
l_t=\alpha x_t+\left( 1-\alpha \right) \left( l_{t-1}+\phi b_{t-1} \right)\\
b_t=\beta \left( l_t-l_{t-1} \right) +\left( 1-\beta \right) \phi b_{t-1}\\
\hat{x}_{t+h}=l_t+\left( \phi +\phi ^2+\cdots +\phi ^h \right) b_t, h=1, 2, \cdots\\
\end{cases}
$$

其中$\phi$就是所谓的阻尼参数，$0<\phi \leqslant 1$，如果$\phi = 1$，则阻尼趋势模型就是霍特线性趋势模型

简单季节性

名称：简单季节性
适用条件：含有稳定的季节成分、不含趋势
与之类似的ARIMA模型：SARIMA(0, 1, 1) × (0, 1, 1)s

$$
\begin{cases}
l_t=\alpha \left( x_t-s_{t-m} \right) +\left( 1-\alpha \right) l_{t-1}\\
s_t=\gamma \left( x_t-l_{t-1} \right) +\left( 1-\gamma \right) s_{t-m}\\
\hat{x}_{t+h}=l_t+s_{t+h-m\left( k+1 \right)}, k=\left[ \frac{h-1}{m} \right]\\
\end{cases}
$$

第一个方程为水平平滑方程，第二个方程为季节平滑方程，第三个方程为预测方程

$m$为周期长度，月度数据为12，季度数据为4，$\gamma$为季节平滑参数，$h$为预测超前期数

温特加法模型

名称：温特加法模型
适用条件：含有线性趋势和稳定的季节成分
与之类似的SARIMA模型：SARIMA(0, 1, 0)×(0,1, 1)s

$$
\begin{cases}
l_t=\alpha \left( x_t-s_{t-m} \right) +\left( 1-\alpha \right) \left( l_{t-1}+b_{t-1} \right)\\
b_t=\beta \left( l_t-l_{t-1} \right) +\left( 1-\beta \right) b_{t-1}\\
s_t=\gamma \left( x_t-l_{t-1}-b_{t-1} \right) +\left( 1-\gamma \right) s_{t-m}\\
\hat{x}_{t+h}=l_t+hb_t+s_{t+h-m\left( k+1 \right)}, k=\left[ \frac{h-1}{m} \right]\\
\end{cases}
$$

加入了$\beta$作为趋势的平滑参数

温特乘法模型

名称：温特乘法模型
适用条件：含有线性趋势和不稳定的季节成分
与之类似的ARIMA模型：不存在

$$
\begin{cases}
l_t=\alpha \frac{x_t}{s_{t-m}}+\left( 1-\alpha \right) \left( l_{t-1}+b_{t-1} \right)\\
b_t=\beta \left( l_t-l_{t-1} \right) +\left( 1-\beta \right) b_{t-1}\\
s_t=\gamma \frac{x_t}{l_{t-1}+b_{t-1}}+\left( 1-\gamma \right) s_{t-m}\\
\hat{x}_{t+h}=\left( l_t+hb_t \right) s_{t+h-m\left( k+1 \right)}, k=\left[ \frac{h-1}{m} \right]\\
\end{cases}
$$

参数均和前面相同

一元时间序列分析的模型

以上就是所有SPSS中支持的指数平滑模型了，知道大概的样子就行了，这块不用深究。下面介绍一些常用的概念，不过都只是大概的，如果弄不懂也无所谓，重心放在运用上就行。

时间序列的平稳性

时间序列$\left\{ x_t \right\}$若满足以下三个条件：

$E\left( x_t \right) =E\left( x_{t-s} \right) =u$，均值均为固定常数
$Var\left( x_t \right) =Var\left( x_{t-s} \right) =\sigma ^2$，方差均存在且为常数
$Cov\left( x_t, x_{t-s} \right) =\gamma$，协方差只与间隔$s$有关，与$t$无关

则称$\left\{ x_t \right\}$，为协方差平稳，又称为弱平稳

如果多余任意的$t_1,t_2,\cdots ,t_k$和$h$，多维随机变量$\left( x_{t1},x_{t2},\cdots ,x_{tk} \right)$和$\left( x_{t1+h},x_{t2+h},\cdots ,x_{tk+h} \right)$的联合分布相同，则称$\left\{ x_t \right\}$平稳。

严格平稳的要求非常高，因此在时间序列中提到的平稳没有特殊说明默认为弱平稳。

若时间序列满足下面的三个条件：

$E\left( x_t \right) =E\left( x_{t-s} \right) =0$
$Var\left( x_t \right) =Var\left( x_{t-s} \right) =\sigma ^2$
$Cov\left( x_t, x_{t-s} \right) =0$

也就是说，如果一个时间序列，其均值为0，方差存在且为常数，协方差与间隔s有关且为0，则称该时间序列为白噪声序列。

差分方程

将某个时间序列变量表示为该变量的滞后项、时间和其他变量的函数，这样的一个函数方程被称为差分方程。

如自回归AR(p)模型：$y_t=\alpha _0+\alpha _1y_{t-1}+\alpha _2y_{t-2}+\cdots +\alpha _py_{t-p}+\varepsilon _t$
移动平均MA(q)模型：$y_t=\varepsilon _t+\beta _1\varepsilon _{t-1}+\beta _2\varepsilon _{t-2}+\cdots +\beta _q\varepsilon _{t-q}$
自回归移动平均ARMA(p, q)模型：$y_t=\alpha _0+\sum_{i=1}^p{a_iy_{t-i}}+\varepsilon _t+\sum_{i=1}^q{\beta _i\varepsilon _{t-i}}$
用其他变量表示：$y_t=a+by_{t-1}+cz_t+dz_{t-1}+\varepsilon _t$
用时间$t$表示：$y_t=a+by_{t-1}+ct+\varepsilon _t$

差分方程的其次部分：只包含改该变量自身和它的滞后项的式子

差分方程的特征方程

对于ARMA(p, q)模型来讲：$y_t=\alpha _0+\sum_{i=1}^p{a_iy_{t-i}}+\varepsilon _t+\sum_{i=1}^q{\beta _i\varepsilon _{t-i}}$

他的其次部分为：$y_t=\sum_{i=1}^p{\alpha _iy_{t-i}}$

将其次部分转换为特征方程：令$y_t=x^t$后带入齐次方程化简：

因为$y_t=x^t$，所以$y_{t-i}=x^{t-i}$，带入后，再将左右两边同时除以$x^{t-p}$即可

$$
x^t=\sum_{i=1}^p{\alpha _ix^{t-i}}\Rightarrow x^p=\alpha _1x^{p-1}+\alpha _2x^{p-2}+\cdots +\alpha _p
$$

特征方程是一个$p$阶的多项式，对应可以求出$p$个解，这个解的模长（实根取绝对值，虚根取模长）的大小决定了形成ARMA(p, q)模型的$\left\{ y_t \right\}$是否平稳。

滞后算子

用$L$表示滞后算子(lag operator)：$L^iy_t=y_{t-i}$，且有如下性质

$LC=C$（$C$为常数）
$\left( L^i+L^j \right) y_t=y_{t-i}+y_{t-j}$
$L^iL^jy_t=y_{t-i=j}$

滞后算子其实是一个方便我们观察序列的符号，比如ARMA(p, q)模型，如果用滞后算子表示：

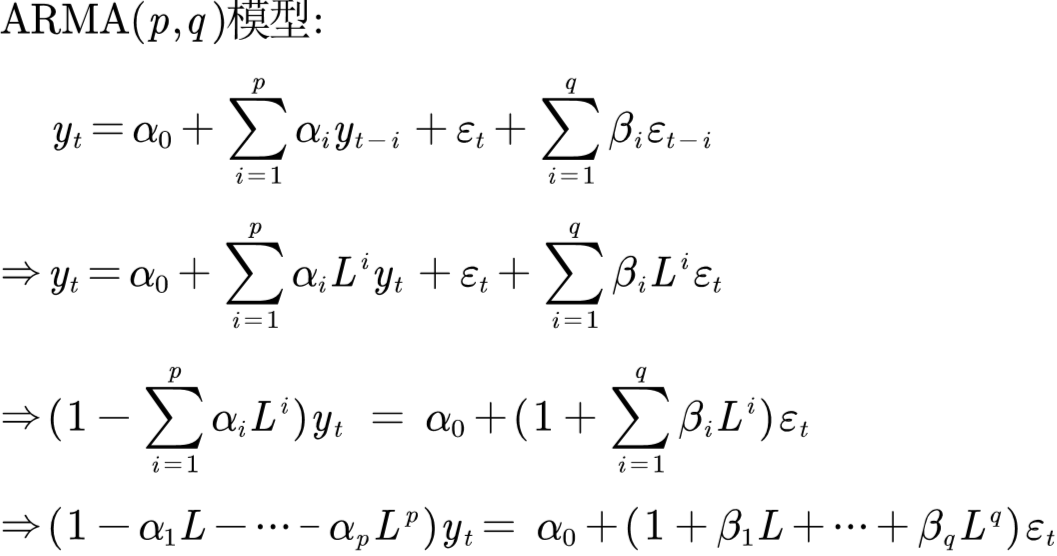
滞后算子的另一个用处就是差分方程，如果我们的时间序列不平稳，我们想将其转换成平稳的序列，常用的手段就是差分

一阶差分：$\Delta y_t=y_t-y_{t-1}=\left( 1-L \right) y_t$

二阶差分：

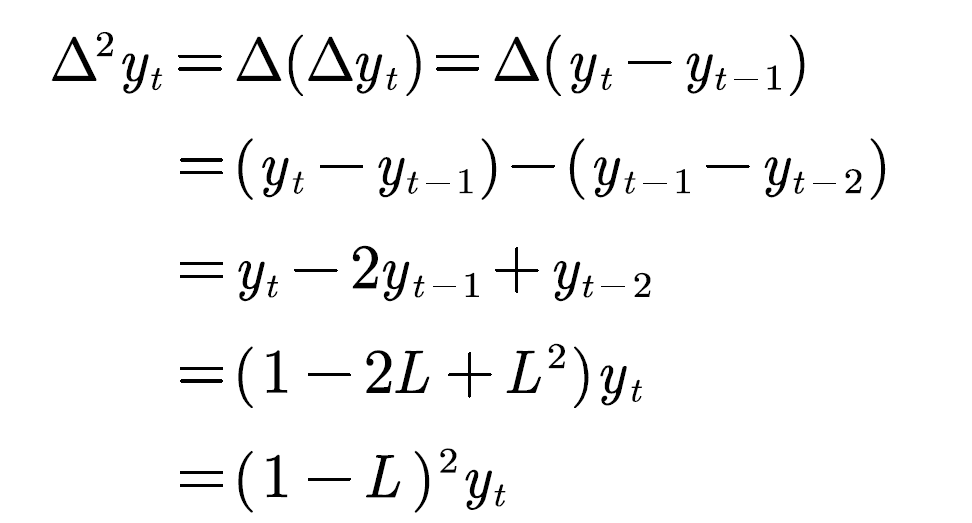
d阶差分：$\Delta ^d\left( 1-L \right) ^dy_t$

AR(p)模型

$p$阶自回归模型：$y_t=\alpha _0+\alpha _1y_{t-1}+\alpha _2y_{t-2}+\cdots +\alpha _py_{t-p}+\varepsilon _t$

其中$\varepsilon _t$是方差为$\sigma ^2$的白噪声序列，所谓的自回归：就是将自己的1至p阶滞后项视为变量来进行回归，这就可能出现一个问题：自相关，一般来讲回归模型的扰动存在两种情况，一种是异方差（横截面数据），另一种就是自相关（时间序列数据）。

自回归只能适用于预测与自身前期相关的经济现象，即受自身历史因素影响较大的经济现象，如矿的开采量，各种自然资源产量等。对于受社会因素影响较大的经济现象，不宜采用自回归，而应使用可纳入其他变量的向量自回归模型（多元时间序列）。

这里要注意：我们讨论的AR(p)模型一定是平稳的时间序列模型，如果原数据不平稳也要先转换为平稳的数据才能再进行建模。

AR(p)模型平稳的条件

对于一个AR(p)模型：$y_t=\alpha _0+\alpha _1y_{t-1}+\alpha _2y_{t-2}+\cdots +\alpha _py_{t-p}+\varepsilon _t$，我们先将其次部分转换成特征方程：$x^p=\alpha _1x^{p-1}+\alpha _2x^{p-2}+\cdots +\alpha _p$ （左右两边同时除以\(x^{t-p}\即可)

根据特征方程的根：

如果这p个解的模长均小于1，则$\left\{ y_t \right\}$平稳，我们也称$\left\{ y_t \right\}$对应的AR(p)模型平稳
如果这p个解中有k个解的模长等于1，则$\left\{ y_t \right\}$为k阶单位根过程（k阶单位根可经过k阶差分变为更平稳的时间序列）
如果这p个根中至少有一个的模长大于1，则$\left\{ y_t \right\}$为爆炸过程，序列指数增长。

MA(q)模型

$q$阶移动平均过程(MA(q)模型)：

$y_t=\varepsilon _t+\beta _1\varepsilon _{t-1}+\beta _2\varepsilon _{t-2}+\cdots +\beta _q\varepsilon _{t-q}$

其实就是对扰动项进行移动平均

对于MA(q)模型，只要q为常数，那么就一定是平稳的，这个可以证明，太麻烦了，我在这里就不写了，因为本身我也看蒙了......

ARMA(p, q)

自回归移动平均模型(Autoregressive Moving Average,ARMA)，就是设法将自回归过程AR和移动平均过程MA结合起来，共同模拟产生既有时间序列样本数据的那个随机过程的模型。

ARMA(p, q)模型：$y_t=\alpha _0+\sum_{i=1}^p{a_iy_{t-i}}+\varepsilon _t+\sum_{i=1}^q{\beta _i\varepsilon _{t-i}}$

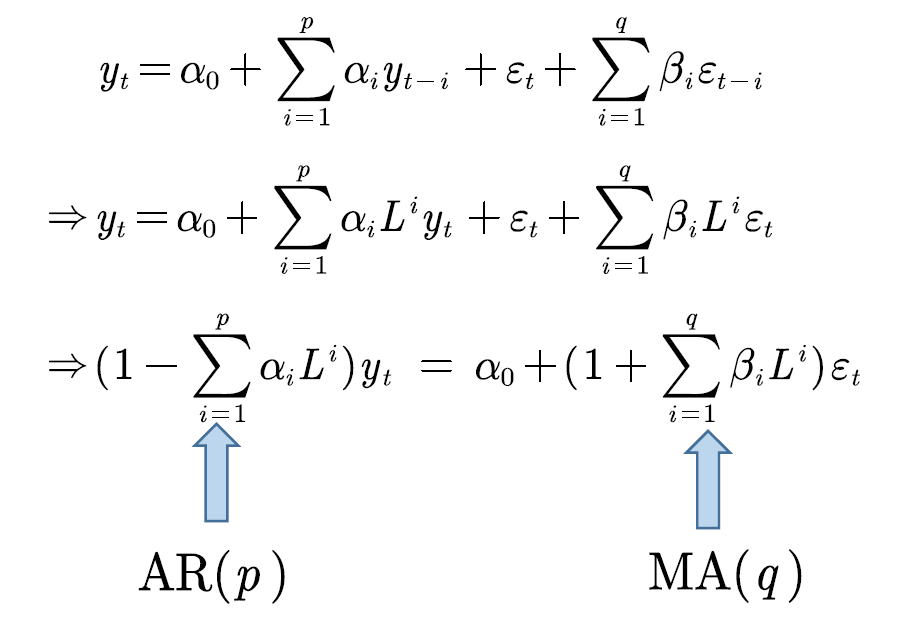
ARMA(p, q)模型的平稳性

前面说过，只要q为常数，那么MA(q)就一定是平稳的，所以在这里，ARMA(p, q)的平稳性只与AR(p)部分有关，前面说过，将其次部分转换成特征方程，然后求根判断：

如果这p个解的模长均小于1，则$\left\{ y_t \right\}$平稳，我们也称$\left\{ y_t \right\}$对应的AR(p)模型平稳
如果这p个解中有k个解的模长等于1，则$\left\{ y_t \right\}$为k阶单位根过程（k阶单位根可经过k阶差分变为更平稳的时间序列）
如果这p个根中至少有一个的模长大于1，则$\left\{ y_t \right\}$为爆炸过程，序列指数增长。

一般，我们可以通过观察时序图来判断时间序列是否平稳，当然，也有相应的假设检验方法能帮助我们对数据的平稳性进行检验（由于第三种情况几乎不会发生，因此我们只需要检验时间序列是单位根还是平稳的即可）

自相关系数ACF

ACF和PACF一样，是用来估计p和q的/

我们在小学二年级学过《概率论与数理统计》，应该都知道啥是相关系数：对于两个随机变量$X$和$Y$：

$$
\rho =\frac{cov\left( X,Y \right)}{\sqrt{Var\left( X \right)}\sqrt{Var\left( Y \right)}}
$$

则称$\rho$为两个随机变量的相关系数。

而自相关系数（autocorrelation）：我们探讨的时间序列首先是平稳的，定义相关系数：

$$
\rho =\frac{cov\left( x_t,x_{t-s} \right)}{\sqrt{Var\left( x_t \right)}\sqrt{Var\left( x_{t-s} \right)}}=\frac{\gamma _s}{\gamma _0}
$$

注意：$\gamma _0=Cov\left( x_t,x_t \right) =Var\left( x_t \right)$

我们将$\rho_s$视为$s$的函数，我们称该函数为自相关函数，其函数图像称为自相关图，自相关系数$\rho_s$表示了一个平稳序列$\left\{ x_t \right\}$中，间隔$s$期的两个时间点之间的相关系数，因为真实的自相关系数我们是不知道的，所以我们只能依赖样本数据来估计，样本自相关系数：

$$
r_s=\hat{\rho} _s=\frac{\sum_{t=s+1}^T{\left( x_t-\overline{x} \right) \left( x_{t-s}-\overline{x} \right)}}{\sum_{t=1}^T{\left( x_t-\overline{x} \right) ^2}}
$$

注意，如果$\left\{ x_t \right\}$为白噪声序列，那么：

$$
\rho _s=\begin{cases}
1 \quad s=0\\
0 \quad s\ne 0\\
\end{cases}
$$

偏自相关系数PACF

我们计算的自相关系数，反应的是$x_t$和$x_{t-s}$这两个间隔时长为$s$的取值的线性相关程度，例如：$x_1$和$x_3$这两个时间点的取值之间的线性相关程度为$\rho_2$，这个线性相关程度不是直接的，他的大小可能会受到中间时刻$x_2$的影响，而偏自相关系数就是来衡量$x_t$和$x_{t-s}$在剔除掉了所有中间取值后得线性关系。

至于计算，就交给SPSS吧~

模型选择：AIC和BIC标准

现在，假设我们通过ACF和PACF已经将p和q估计了一些出来，接下来要做的事就是在这里面选择最优的。

AIC：赤池信息准则（Akaike Information Criterion, AIC）：

AIC = 2（模型中参数的个数）- 2ln（模型的极大似然函数值）

BIC：贝叶斯信息准则（Bayesian Information Criterion, BIC）：

BIC = ln（T）（模型中参数的个数）-2ln（模型的极大似然函数值）

其中的T是样本个数，n是模型中的参数（反映模型的复杂程度），极大似然函数值反映模型对于数据解释（拟合）的程度

AIC和BIC都是取小原则，我们要选择使得AIC或BIC最小的模型。

检验模型是否识别完全

估计完成时间序列模型后，我们需要对残差进行白噪声检验，如果残差是白噪声，则说明我们选取的模型能完全识别出时间序列数据的规律，即模型可接受；如果残差不是白噪声，则说明还有部分信息没有被模型所识别，我们需要修正模型来识别这一部分的信息。

如果$\left\{ \varepsilon \right\}$是白噪声序列，那么：$\rho _s=\begin{cases}
1 \quad s\,\,=\,\,0\\
0 \quad s\,\,\ne \,\,0\\
\end{cases}$ ，样本自相关系数：

$$
r_s=\hat{\rho}_s=\frac{\sum_{t=s+1}^T{\left( x_t-\overline{x} \right) \left( x_{t-s}-\overline{x} \right)}}{\sum_{t=1}^T{\left( x_t-\overline{x} \right) ^2}}
$$

Ljung and Box在1978年提出的Q检验可以帮助我们检测残差是否为白噪声：$H_0:\rho _1=\rho _2=\cdots =\rho _s=0, H_1:\rho _i$中至少有一个不为0，使用SPSS，会帮我们计算出p值，p值小于0.05会拒绝原假设，此时模型没有识别完全，需要修正。

ARIMA(p, d, q)模型(差分自回归移动平均模型)

在此之前，我们都探讨的是(\left\{ y_t\right\}\)是平稳的时间序列，而有时候时间序列可能是d阶单位根过程，所以，我们需要先对数据进行差分处理，将其转换成平稳的时间序列后再进行建模。

ARIMA(p, d, q)模型：

$$
y_{t}^{'}=\alpha _0+\sum_{i=1}^p{\alpha _iy_{t-i}^{'}}+\varepsilon _t+\sum_{i=1}^q{\beta _i\varepsilon_{t-1}}
$$

使用差分方程表示：$y_{t}^{'}=\Delta ^dy_t=\left( 1-L \right) ^dy_t$

SARIMA(Seasonal ARIMA)模型

到目前为止，我们只关注非季节性数据和非季节性ARIMA模型，然而，ARIMA模型也能够对广泛的季节数据进行建模。

季节性ARIMA模型是通过再ARIMA模型中包含额外的季节性项而生成的，形式如下

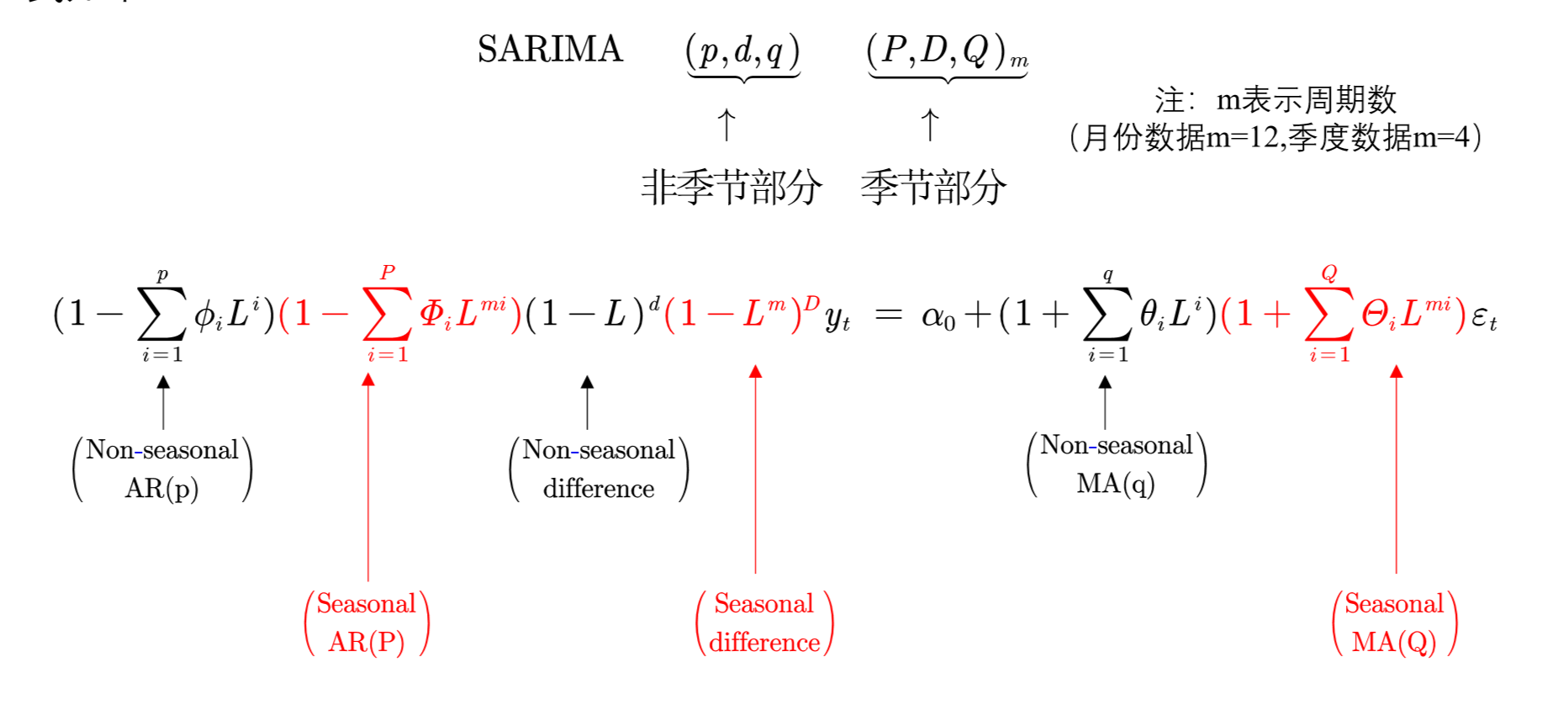
原理部分非常麻烦，博主很多地方也云里雾里，不过不要紧，计算过程我们都可以交给SPSS，我们将重点放在分析就好了~