数学建模中,常常需要根据一致的函数点进行数据、模型的处理和分析,而有时候现有的数据是极少的,不足以支撑分析的进行,这时就需要使用一些数学的方法,“ 模拟产生 ”一些新的但又比较靠谱的值来满足需求,这就是插值的作用,我在这里简要介绍两种常用的插值方法。
分段三次埃尔米特插值
Matlab内置了函数,如果不是数学专业的会用就行。
P = pchip(x, y, new_x)
x是已知点的横坐标;y是一直点的纵坐标;new_x是要插入对应的横坐标,例如:
x = -pi:pi; y = sin(x); new_x = -pi:0.1:pi; p = pchip(x, y, new_x); plot(x, y, 'o', new_x, p, 'r-') %r-表示红色的折线 %% 解释: -pi:pi 表示从-3.14到3.14,每次的增量为1 -pi:0.1:pi 表示的是从-3.14到3.14,每次的增量为0.1 plot函数: plot(x1, y1, x2, y2) 线方式:-表示实线 -.表示虚点线 --波折线 点方式:.原点 +加号 *星号 x x型 o小圆(就是上面用的) 颜色:y黄;r红;g绿;b蓝;w白;k黑;m紫;c青
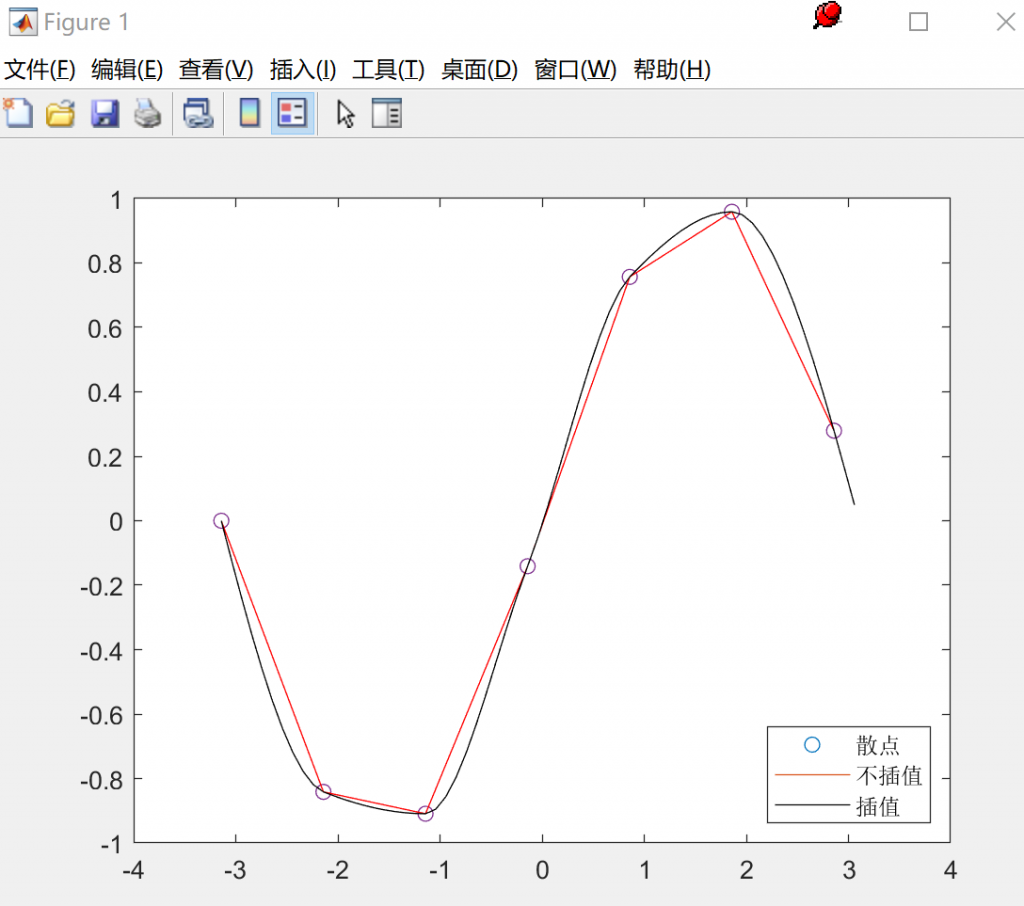
三次样条插值(更加精确)
前提:需要函数是一个三次多项式,还要求函数二阶连续可微。
Matlab也有内置的函数:p = spline(x , y , new_x)
x是已知的样本点横坐标;y是已知样本点的纵坐标;new_x是要插入处对应的横坐标,例如:
x = -pi:pi; y = sin(x);
new_x = -pi:0.1:pi;
p1 = pchip(x, y, new_x); %分段三次埃尔米特插值
p2 = spline(x, y, new_x); %三次样条插值
plot(x, y, 'o', new_x, p1, 'r-', new_x, p2, 'b-')
legend('散点','三次埃尔米特插值','三次样条插值','Location','SouthEast')
%%解释
spline即为三次样条插值的函数
legend('string 1', 'string2', 'string3',...)
分别将字符串1,字符串2,字符串3...标注到图中,每个字符串对应的图标为画图时的图标
‘Location’用来指定标注显示的位置
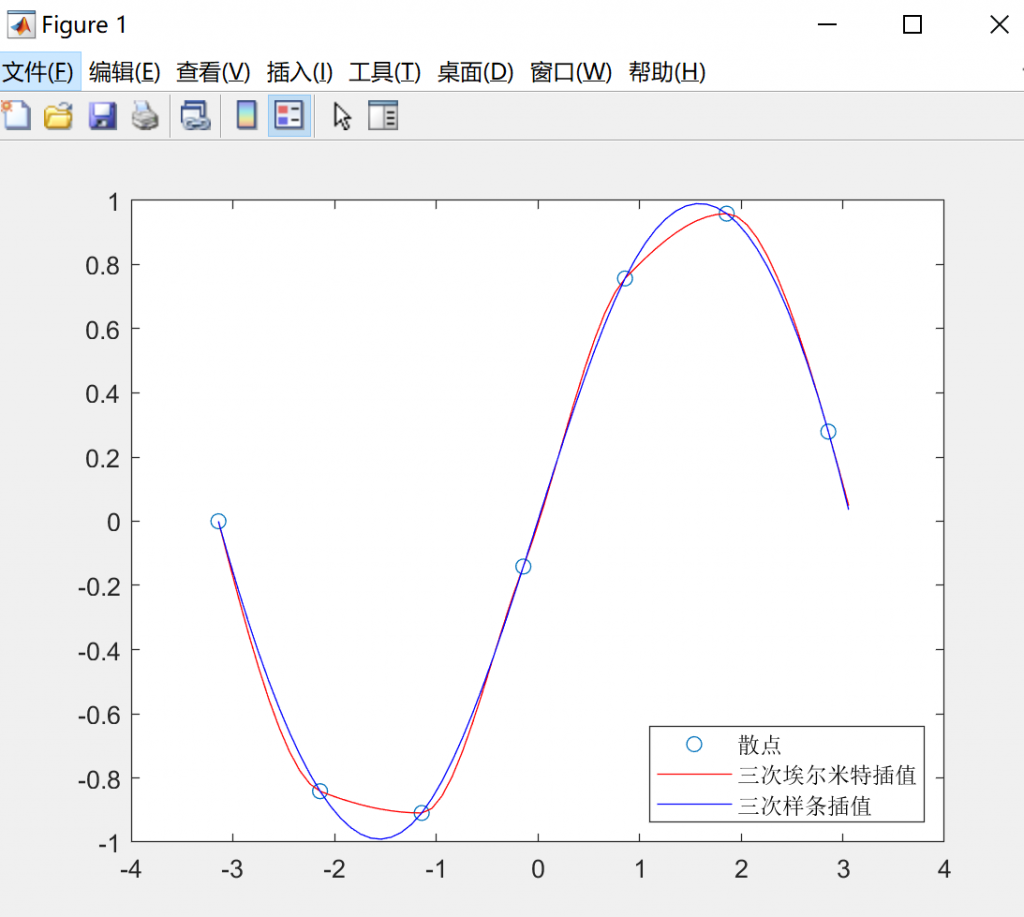
可以看出三次样条插值生成的曲线更加光滑
插值算法还可用于短期预测!!(不展开)







Comments 1 条评论
学习一波