《JCSP: Joint Caching and Service Placement for Edge Computing Systems》论文阅读

边缘计算课程汇报论文，精读一波

Abstract

在资源受限的情况下，边缘计算系统中的缓存问题——即缓存什么、在哪里缓存以及如何缓存——是一个关键挑战。缓存的项目不仅包括应用数据内容，还包括处理传入请求的边缘服务的本地缓存。然而，当前的系统将内容和服务分开管理，没有考虑缓存和排队延迟之间的相互作用。因此，本文提出了一种新颖的随机模型类别，使得内容缓存和服务放置决策可以联合优化。我们首先解释了如何应用分层排队网络（LQNs）模型进行边缘服务放置，并展示了将其与遗传算法结合可以在资源分配的准确性上比现有基线方法有更高的提升。接下来，我们将缓存组件扩展到LQNs中，建立了一个联合内容缓存和服务放置（JCSP）的建模方法，并提出了分析结果模型的分析方法。最后，我们模拟了真实世界的Azure追踪数据来评估JCSP方法，并发现与基线启发式方法相比，JCSP在响应时间上可以达到高达35%的改进，并且在内存使用上可以减少500MB。

现有的边缘计算系统在处理缓存和服务放置时通常是分开的，没有考虑到它们之间可能存在的延迟影响。为了解决这个问题，论文提出了一种新的建模方法，即联合缓存和服务放置（JCSP），通过这种方法可以同时考虑缓存和服务放置的决策，以优化边缘计算资源的使用。

数据内容：通常是用户的请求数据，视频、网页、图片、文件等，在边缘计算中，这些内容可以被缓存在离用户更近的边缘节点上，减少传输时间，提高数据检索的速度

加入缓存：存储频繁访问的内容在边缘节点上，再次请求的时候可以快速提供，不需要每次都从数据中心拉取

计算服务：执行数据处理、分析、转换等任务的应用程序或软件服务。在边缘计算中，这些服务被部署在边缘节点上，就近处理数据，减少延迟

所谓将内容和服务分开管理，指的是传统的边缘计算系统可能将内容缓存（如数据文件的存储）和服务放置（如数据处理程序的运行位置）作为两个独立的问题来处理。这意味着系统可能优化了数据的存储位置，但没有考虑到这些数据如何被处理服务使用，或者反之。

用户请求的处理通常需要两个步骤：首先是从缓存中检索数据内容，然后是将这些数据送到服务进行处理。如果系统仅优化了内容的缓存位置，而没有考虑服务处理的位置和排队等待时间，那么即使数据很快被检索出来，但如果处理服务的排队延迟很长，用户仍然会面临较高的总体延迟。

因此本文最主要的贡献点就在于内容缓存（数据）与服务放置（计算）之间的联动优化。

1. INTRODUCTION

在过去的十年里，许多类型的智能应用程序，如虚拟现实、互动游戏和面部识别，已经迅速发展。这些计算密集型应用程序不断地被期望满足高数据速率并满足不断增长的用户需求所引起的服务质量（QoS）要求。然而，这些应用程序的效率和可靠性都受到终端设备在存储、电池寿命和计算能力方面的限制。因此，为了避免在处理传入任务时出现高延迟，计算要求高的工作通常会被卸载到云数据中心后端以实现更快的执行。

然而，这种方法面临着响应时间长的问题，因为从终端用户到数据中心的传输距离可能相当大。这对于对延迟敏感的应用程序，如自动驾驶和实时视频来说是个问题。在这种情况下，从集中式云计算自然过渡到分布式边缘计算的范式转变已经发生。边缘计算在网络边缘配置计算、存储和带宽资源，例如基站和接入点，靠近终端用户。通过这些手段，边缘计算提供了显著降低延迟的优势。

在本文中，我们关注边缘缓存策略，即在资源有限的情况下，如何在边缘满足用户需求进行缓存，包括缓存什么、在哪里缓存以及如何缓存，这是边缘计算的关键使能技术之一。传统的缓存在代理服务器或靠近终端用户的服务器上存储项目副本，如图像、文件和脚本。与传统缓存不同，边缘缓存将项目存储在接近的网络边缘，如小型蜂窝基站（SBSs）和车辆。此外，缓存的项目不再仅限于数据内容，还可能包括决定在特定边缘资源上部署哪些服务以执行的决策。具体来说，内容缓存被提出来解决内容放置和交付的问题。而服务放置指的是在边缘服务器上部署服务及其相关数据库，以执行从终端用户卸载的任务。

在现有研究中，边缘内容缓存专注于数据缓存，没有考虑在放置用于处理它的服务时的排队竞争。同样，边缘服务放置通常忽视了内容缓存在服务执行延迟中所起的作用。为了解决这两个问题，我们提出了一种联合缓存和排队的方法，包括一类新的模型和相应的资源分配方法。这些模型的独特之处在于能够随机模拟服务访问排队和缓存命中/未命中的延迟相互作用。为了实现这一类新的随机模型，我们推广了一类称为分层排队网络（LQNs）的模型，这些模型用于分层服务架构的性能工程。我们的扩展首次在这些模型中整合了缓存特性，从而开发了一种新的边缘系统随机调度工具。具体来说，我们的主要贡献如下：

我们首先通过分层排队网络（LQNs）对基本的作业调度和服务放置过程（忽略缓存）进行建模。应用于随机工作负载，我们在实验中发现，与[9]中的确定性调度方法相比，系统响应时间平均提高了16%。这证明了采用LQN形式主义来处理随机调度的好处。
我们将带有缓存组件的LQN模型进行了推广，这建立了一种边缘内容缓存和服务放置（JCSP）的联合建模方法，并提出了分析该推广模型的解析算法。
我们模拟了一个基于高级排队Petri网（QPN）的模型来验证所提出的集成LQN-缓存模型类的准确性，并在LINE 2工具[10]中实现了推广的LQN模型。
我们基于真实世界的Azure追踪数据进行了广泛的模拟，以评估我们提出的JCSP方法的适用性。结果表明，在广泛的情况下，与基线相比，JCSP方法可以在系统响应时间和内存消耗之间找到更好的平衡。

本文的结构如下。第二部分，我们介绍相关工作并指出其局限性。第三部分，我们发展了方法论。第四部分，我们设计了包含缓存的推广模型，并介绍了解析方法。第五部分给出了模型验证和实验评估。最后，第六部分总结了本文。

2. RELATED WORK

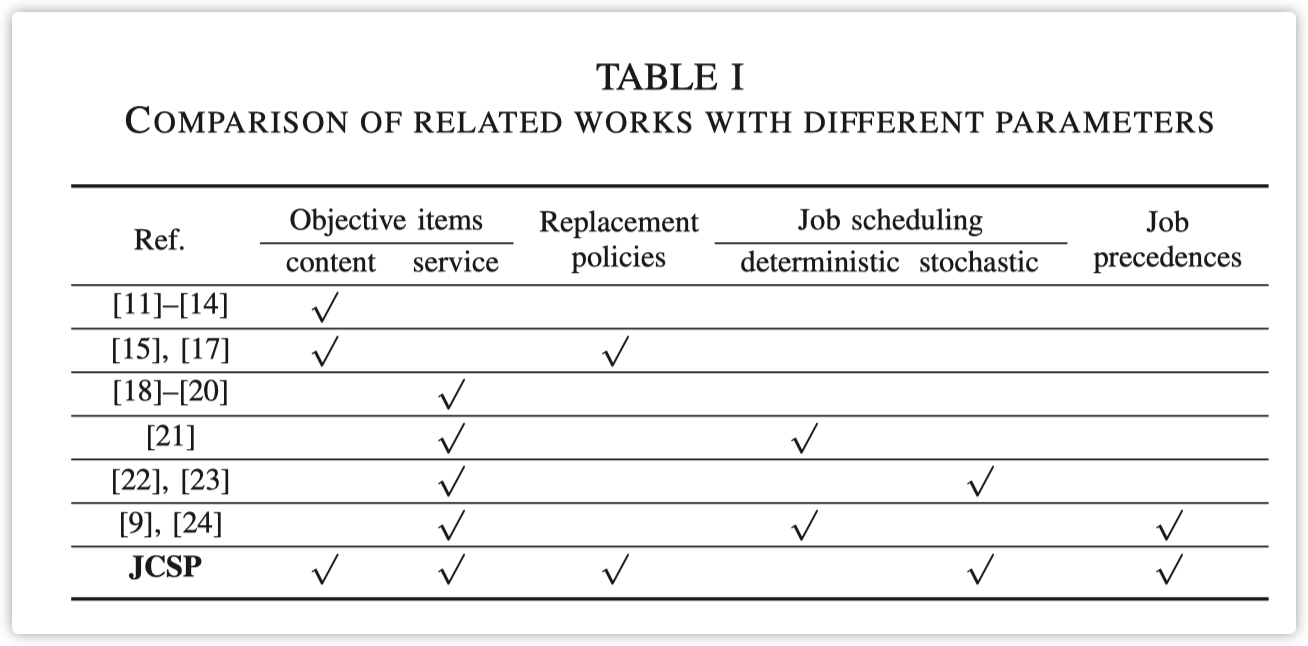
当前研究从两个角度调查了边缘缓存，即内容缓存和服务放置，如TABLE 1所示。边缘内容缓存的基本问题是基于所研究的边缘计算系统的架构特征，优化缓存什么以及如何缓存。关于缓存什么，大多数研究集中在内容流行度特征上，这可以分为已知、未知但静态，以及未知且时变。至于如何缓存，不同的策略在网络拓扑设置上有所不同。在使用传统的两层分层网络时，关键问题是在一定资源限制下，在边缘节点和中心节点之间做出权衡。在采用以用户为中心的结构时，如何在边缘节点群体内协作，如小型蜂窝基站（SBSs）或车辆，是至关重要的。上述关于在边缘节点缓存内容的研究忽略了放置用于处理这些内容的服务。

对于边缘服务放置，现有研究集中在优化系统性能，例如响应时间、能效或成本，这是由于边缘资源的限制。此外，许多研究将服务放置与作业调度过程联合优化。这两个过程是相互作用的，因为放置的服务决定了如何调度作业，而调度策略影响了放置策略的性能。为了联合模型这两个过程，大多数技术利用了排队理论，如$M/G/1$和$M/M/1$。然而，这些模型通常不反映作业之间的优先级。如果考虑优先级约束，大多数方法采用有向无环图（DAG），其最优调度通常是NP-hard的问题，除非具有特定的图拓扑（例如，in-tree入树、out-tree出树）。

在上述研究中，存在两个主要的局限性。首先，对于边缘服务放置，有向无环图（DAGs）有效地模拟了具有先行关系的作业。然而，DAG无法展示作业调用的底层资源依赖性，因为它不包括调度策略和资源争用。因此，我们提出用分层排队网络（LQNs）来联合模型依赖作业调度和服务放置过程。LQNs已被广泛用于模拟具有复杂特性的分布式计算系统，如fork/join交互和多层服务[26]。LQN根据其功能和请求类型将软件和硬件资源分布在多个层次中。当请求需要同时占用资源时[8]，LQN可以通过描述每一层中客户端和服务器之间的交互来明确表示依赖关系。然后，每一层自动转换为马尔可夫排队网络模型，该模型在聚合结果以产生端到端延迟估计之前，被单独分析。因此，如果将LQNs应用于分层边缘计算系统，每个边缘节点可以作为客户端或服务器来请求或提供服务，这使得模型和追踪嵌套依赖性变得简单。

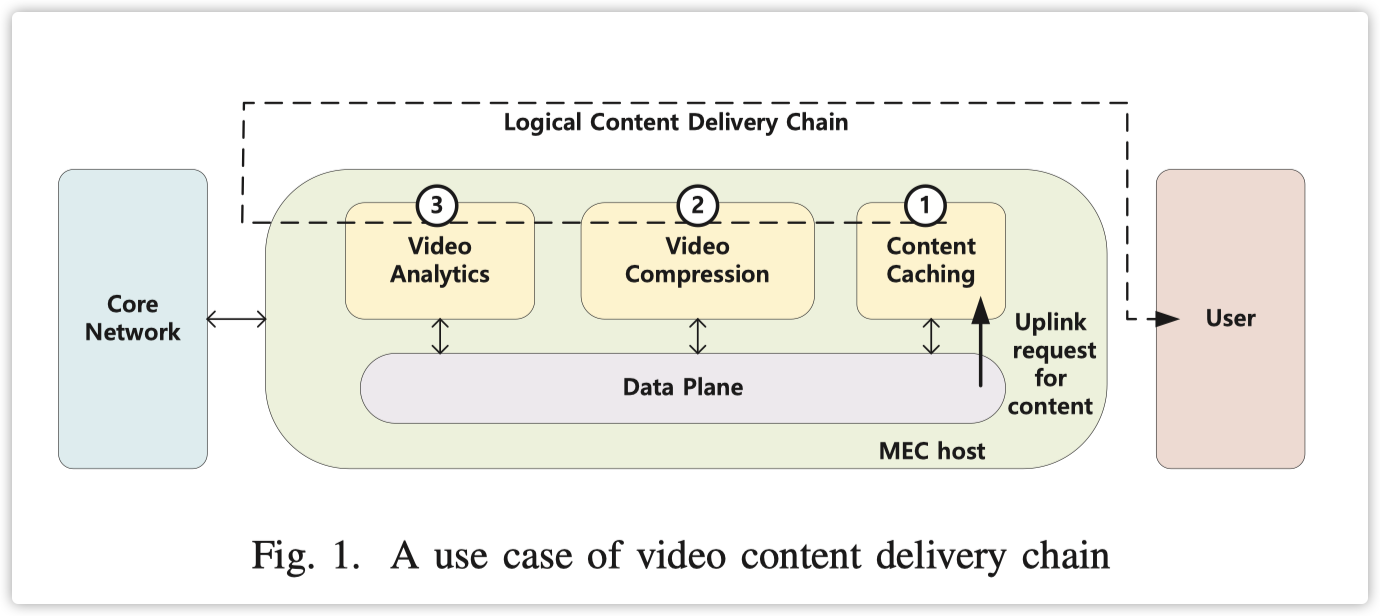
接下来，边缘内容缓存和服务放置过程分别研究。然而，在实践中，许多应用程序的处理既需要计算也需要数据。例如，在视频分析中，请求首先被转发到内容缓存功能以检索缓存的内容。在识别之后，请求被路由到视频压缩和视频分析服务进行进一步处理，如图1所示。因此，我们提出建立一个统一的资源分配方法，同时用于内容和服务。由于我们定义了缓存和LQNs分别模拟内容和服务的处理，关键挑战是如何建立和分析集成的缓存和排队网络模型。

3. METHODOLOGY

3.1 System Model

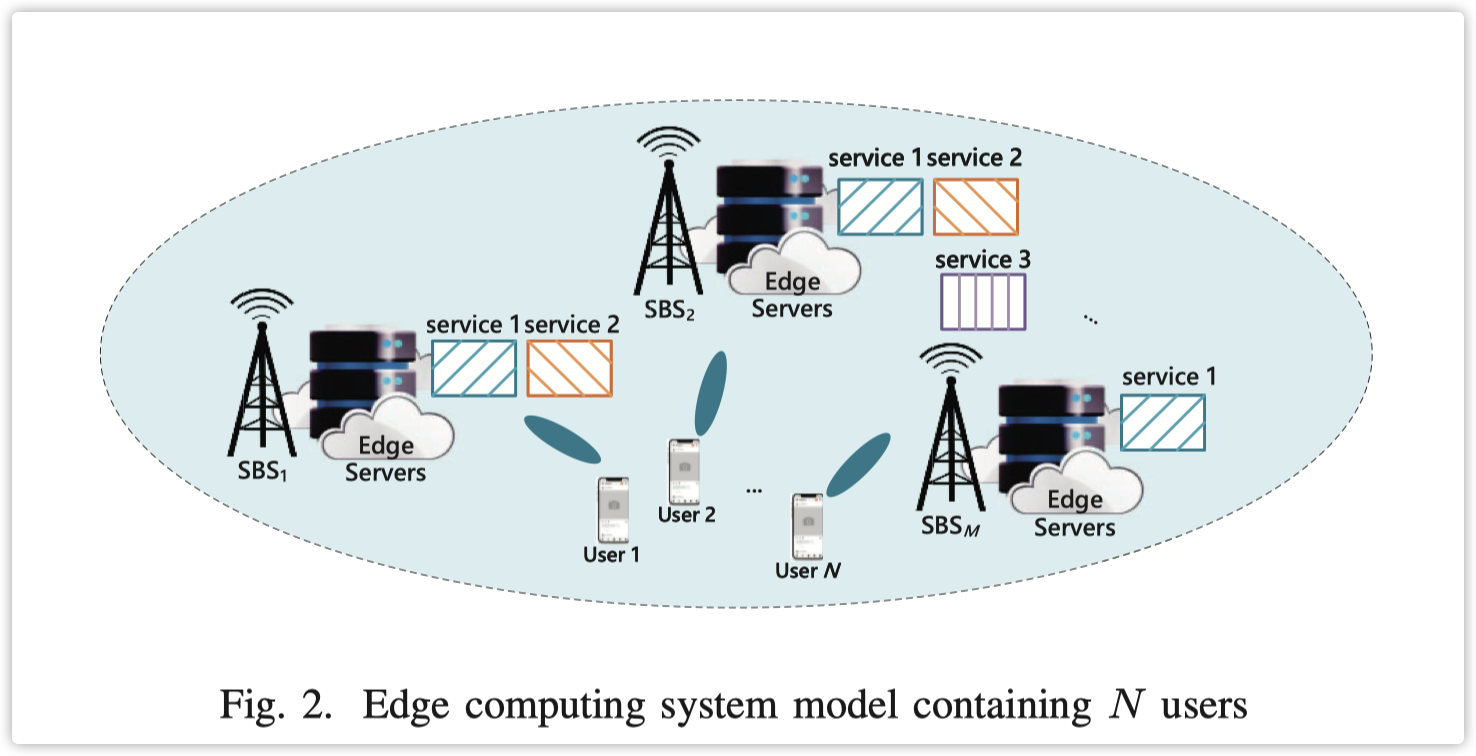
我们考虑一个由M个边缘节点组成的集群，这些节点在边缘计算系统中连接N个用户，如图2所示。每个边缘节点在与小型蜂窝基站（SBSs）共位的边缘服务器中提供多种服务。每个用户将几个作业卸载到连接的边缘节点进行服务。卸载的作业可能有必须按顺序处理的先行关系。例如，一个面部识别应用可以被看作是由五个连续的作业组成，即对象获取、面部检测、预处理、特征提取和分类。每个作业可以单独在提供相应服务的边缘节点上操作。当请求的服务不在连接的边缘节点提供时，需要将作业转发到满足要求的其他边缘节点。此外，同一节点上的不同类型的作业也遵循顺序处理。

我们假设作业总数为$K$，它们请求的可能服务总数为$C$。对于节点$m$上的作业$k，k = 1, 2, …, K$，$m = 1, 2, …, M$，我们定义了两个参数如下：

服务放置决策 $P_{mk}$。如果节点 $m$ 提供作业 $k$ 请求的服务，则$P_{mk}=1$。否则，$P_{mk}=0$。为作业 $k$ 提供服务的所有节点集合表示为$F_k={m|p_{mk}=1, m=1,2,…,M}$
平均服务时间$t_{mk}$，这是作业$k$在访问节点$m$时请求的计算处理量。不同的作业可能请求不同的平均服务时间。

然后我们使用一个分层排队网络（LQN）来模拟作业调度和服务放置问题，如图3所示。每个边缘节点$m$由以下4个组成部分构成：

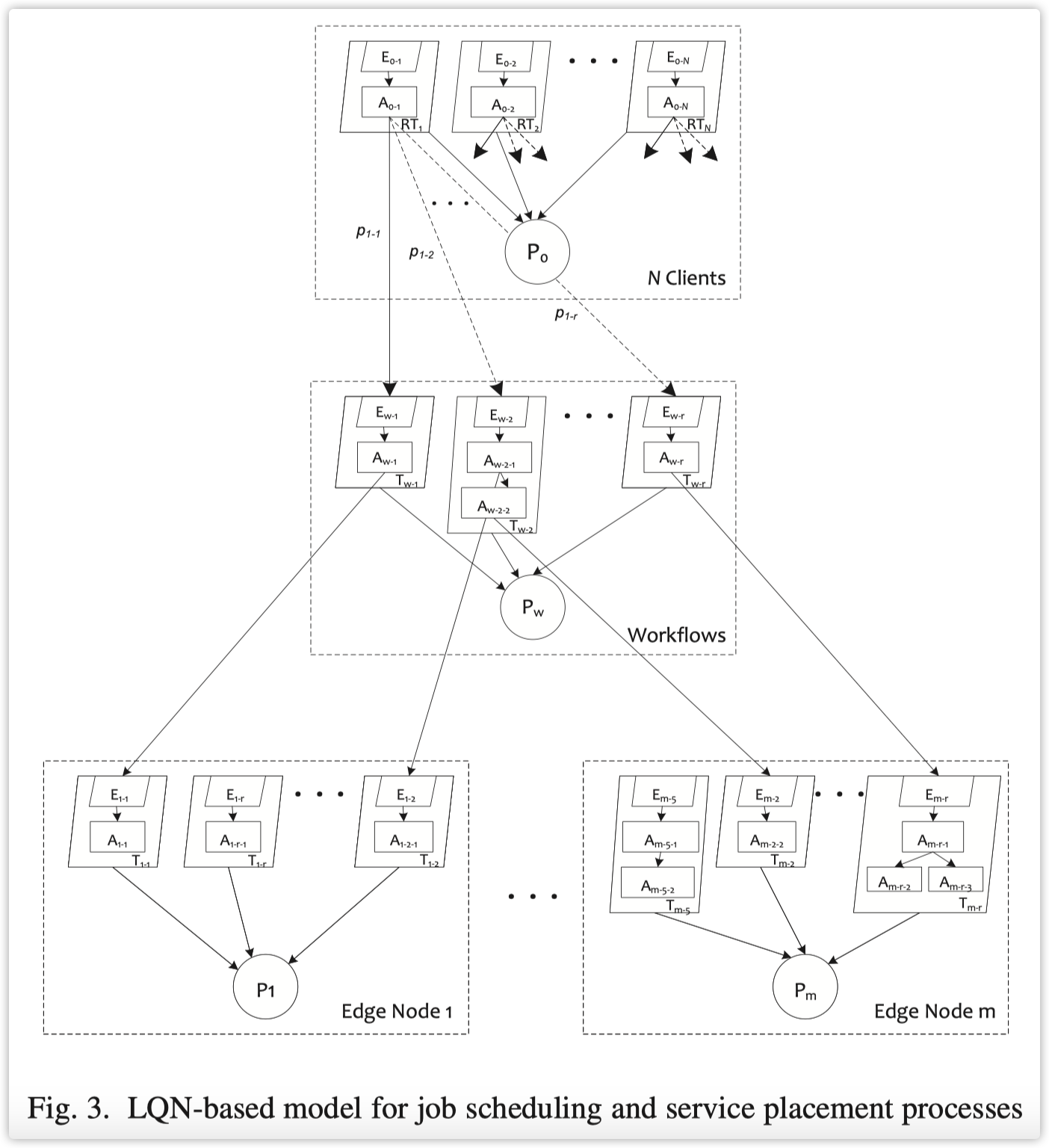
处理器：处理器：小型蜂窝基站（SBS）被建模为一个处理器$P_m$，显示为一个圆圈。它遵循处理器共享调度策略，这是时间共享调度的数学抽象，具有无限小的时间量子。
任务：共位的边缘服务器被建模为一组任务$T_{mc}$，显示为较大的平行四边形，每个平行四边形代表在处理器 $P_m$ 上运行的服务$c$。每个任务都有一个队列来模拟先来先服务（FCFS）的准入控制，服务时间遵循阶段型分布，例如指数分布、Erlang分布或超指数分布。
入口(Entry)：入口：每个任务至少发布一个入口$E_{mcj}$，$1\le j \le J$，显示为一个小平行四边形，它代表对服务$c$调用的终点。通常情况下，一个有$k$个可能终点的服务被建模为一个有$k$个入口的任务。
活动(Activity)：每个入口调用一系列活动 $A_{mci}$，其中$i = 1,…,I_c$且$I_c$是服务$c$的活动数量。活动以一系列矩形的形式展现在入口下方，代表独立或依赖的执行。也就是说，调用一个入口$E_{mcj}$将导致在基础处理器上执行一连串的个别活动。在LQNs中，这样的活动可以以有向无环图（DAG）的形式组织起来，称为活动图，并将在后面详细介绍。注意，每个活动可能通过调用不同的入口到达。

客户端在LQN形式主义中被建模为在伪处理器$P_0$上运行的参考任务。伪处理器是一种类似于处理器的建模抽象，但在边缘系统中没有物理实体，用于保持模型中所有任务的概念上相似的描述。在LQNs中的伪处理器也适合描述用户思考时间。每个客户端请求不同工作流的概率不同。用户工作流也是DAGs，用来表示作业之间的先行关系，并且作为特殊的活动图在伪处理器$P_w$内建模。在$P_w$ 上的无限服务器的平均队列长度被定义为工作流的多重性。如果依赖作业在不同节点执行，活动图将特别显示发出同步调用到不同节点的特殊活动，例如$A_{w-2-1}$和$A_{w-2-2}$。因此，DAGs既出现在参考处理器中以描述用户工作流，也绑定到服务的入口上以描述每个入口启动的活动。后者通常也是DAGs，可能包括对其他任务和入口的同步或异步调用。

3.2 Problem Formulation

我们上面描述的LQN模型允许我们获得吞吐量、响应时间（即，每次调用的延迟）、平均队列长度（即，积压）和每个组件类型的利用率的分析估计。在本文的其余部分，我们专注于响应时间，但其他参考指标也可以很容易地从模型中生成。我们的优化目标是最小化基于LQN模型的端到端总响应时间 $R$，其表示为：$R=\sum_{i=1}^{C}\frac{X_i}{X}R_i$ ，其中 $X_i$，$R_i$ 和$X$分别是作业类别$i$的吞吐量，作业类别$i$的响应时间，以及所有服务类别的总吞吐量之和。比率$X_i/X$可以看作是稳态时到达作业属于类别 $i$ 的概率。因此，依赖作业调度和服务放置的问题被表述为

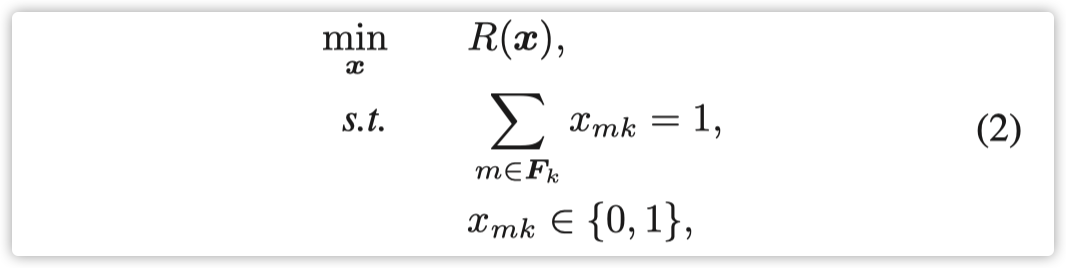
其中$x_{mk}$表示在节点$m$上作业$k$ 的调度决策。向量$x=[x_{11},…,x_{mk},…,x_{MK}]$代表所有作业的一组调度决策，而$R(x)$是带有决策向量$x$的相应系统响应时间。第一个约束保证作业$k$仅在一个（且只有一个）提供所需服务的可行边缘节点上被服务。第二个约束确保如果作业$k$被安排在节点 $m$上服务，那么$x_{mk}=1$，否则$x_{mk}=0$。

4. GENERALIZED LQN MODEL DESIGN

4.1 New Design Formalism

为了将LQN模型扩展以包括缓存组件，我们首先定义以下两个新组件：

缓存任务(cache-task)：在LQN模型中，每个缓存节点被定义为一个缓存任务。每个缓存任务提供通过缓存访问一系列项目的能力，例如键值存储。缓存任务具有任务的基本属性，但增加了四个特定于缓存的属性：项目总数、缓存容量、缓存分区到列表中，以及缓存替换策略，例如最近最少使用（LRU）、最不频繁使用（LFU）、先进先出（FIFO）和随机替换（RR）。
项目条目(item-entry)：缓存模块提供的服务在LQN模型中被定义为项目条目。每个项目条目代表通过缓存任务可访问的项目集合。项目条目类似于标准entry，但增加了item受欢迎程度的属性，例如Zipf分布或自定义分布。

当客户端对缓存任务公开的条目发起调用时，客户端会在缓存命中或未命中后获得所请求的对象。命中/未命中的选择取决于缓存的内容，并且在绑定到该条目的有向无环图（DAG）中表现为不同分支的选择。这通过一种新的优先级关系来建模，即活动图的边缘。我们将这种优先级关系命名为每个条目下的缓存访问，用于缓存命中和未命中活动，这可以用来指定活动图中的分支。缓存访问将传入的作业转换为命中或未命中的作业，并以一定的概率将转换后的作业发送到相应的出站链接。

每个缓存任务的缓存替换策略默认采用随机替换（RR）策略，当发生缓存未命中时，它会随机选择一个候选项目进行替换。随机替换策略可以提供与带有指数计时器的生存时间（TTL）机制相同的稳态性能。因此，它是对现实世界中的TTL机制的一个合理近似，并且具有更好的分析可解性。其他策略，如最近最少使用（LRU）或CLIMB，可以作为我们基本框架的简单扩展得到。

基于这样的扩展，我们通过启用缓存来推广LQN模型。图4展示了一个包含一个缓存任务的LQN模型示例。任务平行四边形中的右上符号用来区分缓存任务和普通任务。当一个项目请求到达时，我们用$p_{hit}$来模型化项目在缓存中的概率，用$p_{miss}=1-p_{hit}$来模型化项目不在缓存中的概率。生成的架构允许将缓存和排队联合模型化到同一个LQN模型中。需要注意的是，$p_{hit}$ 和$p_{miss}$不需要由最终用户指定。它们是通过解决支撑带缓存LQN的随机模型自动确定的，这也依赖于我们在下一节中描述的缓存替换策略的随机平衡分析。

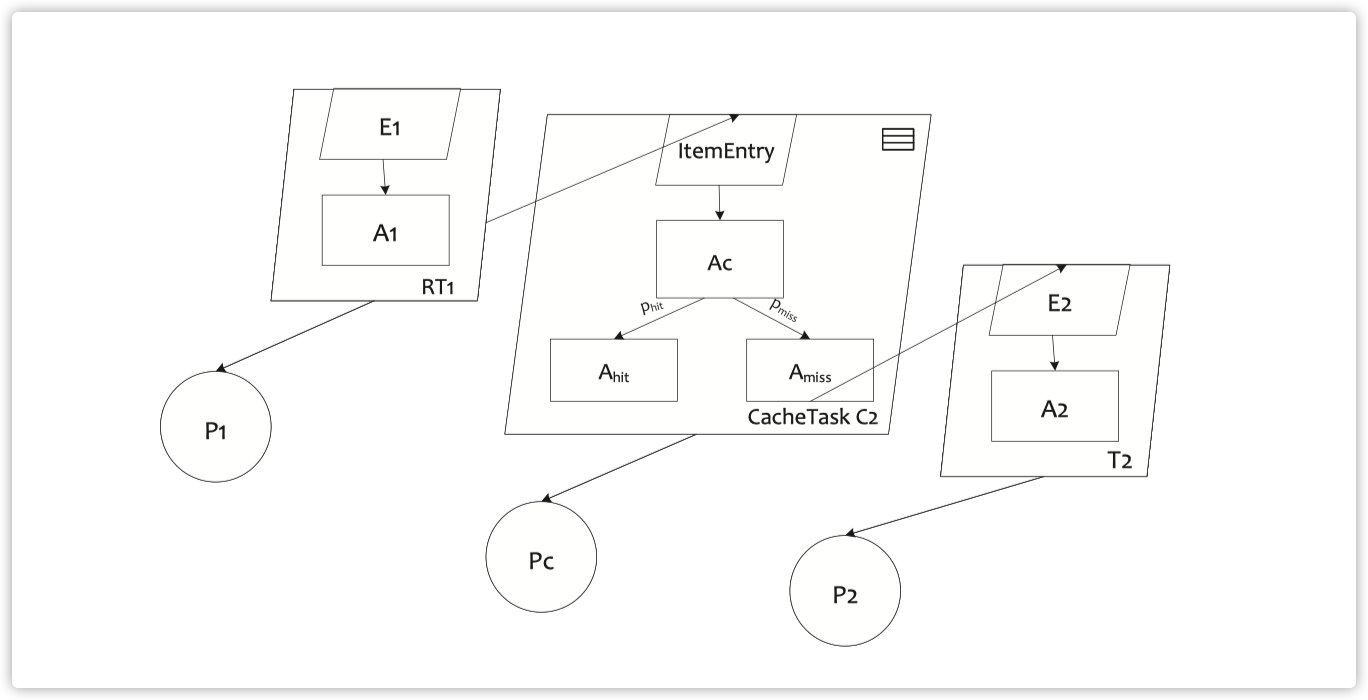
Fig. 4. An example of a LQN model containing one cache-task

4.2 Analysis of LQN Models with Caching

为了解决包含缓存模块的LQN模型，第一步是将整个模型分解为一组子模型。每个子模型可以被视为包含客户端和服务器的混合排队网络。这里的“混合”指的是开放服务类和封闭服务类的同时存在。前者代表来自客户端的异步请求，而后者代表同步请求（即，由于来自有限连接池，所以是封闭的）。特别是，当排队网络包含缓存模块时，工作负载是同步的，这意味着发出下一个对缓存的请求需要在收到对缓存发出的最后一个请求的回复之后进行。为了模拟这种动态，我们进一步将缓存子模型分为两个子模型，如图5所示。在上层子模型中，缓存模块被隔离在一个开放的排队网络中，具有异步的泊松流。而在下层子模型中，延迟和排队站点被包含在一个封闭的排队网络中。

为了解决缓存子模型，我们将[29]中对非分层排队网络的分析方法推广到LQNs的多层设置中。我们给出的方法表达式为了简单起见，只关注单一类别的作业，但我们的实现应用了[29]中为多类别案例开发的类似公式。

在上层子模型中，缓存请求作为单一类别的泊松流到达，其速率为$\lambda=\sum_r\lambda_r$。通过对到达率 λ 的初步猜测，缓存节点的未命中率和命中率，即$p_{miss}^{(t)}$和$p_{hit}^{(t)}$，通过固定点迭代（FPI）方案进行迭代近似。在每次迭代中获得的值在[29]中被利用来通过以下应用小律法则来计算下一个到达率 $λ^{(t+1)}$ ：

$$\lambda^{(t+1)}=\frac{s\lambda^{(t)}}{\lambda^{(t)}\theta_t+p_{miss}^{(t)}\theta_m+p_{hit}^{(t)}\theta_h}$$

其中$θ_t、θ_m、θ_h$分别是平均思考时间、由于未命中和获取项目而产生的平均延迟。这里的$s$是对缓存的挂起请求的最大数量，即缓存子模型中作业的总数。迭代过程持续进行，直到$λ$的值收敛。

在每次迭代中得到的未命中率和命中率被用来作为路由概率来参数化下层子模型的排队网络。也就是说，经历缓存命中的调用代表的作业将在访问缓存后动态切换到命中服务类别，这将按照为命中指定的活动图中的活动由排队站点处理。同样，经历未命中的调用将切换到代表未命中活动图中工作流的未命中服务类别。基于类别切换的命中和未命中调用的分离使得能够模拟两类请求所经历的不同响应时间，这取决于它们访问的项目是否被缓存。在经历了命中/未命中操作链的最后，两类作业将被合并回原始类别，并作为该类别的响应返回给用户。

通过以下方案，上层子模型的解与下层子模型的解通过迭代进行协调：

用过一个随机值来猜测$\lambda_0$
使用近似方法（例如，固定点迭代FPI）解决上层子模型，以获得命中和未命中的概率，即 $p_{hit}$和$p_{miss}$
将 $p_{hit}$ 和 $p_{miss}$ 传递给下层子模型以设置路由矩阵
使用排队网络求解方法 $f(s)$（例如，近似平均值分析AMVA [30]）解决下层子模型，以获得平均吞吐量 $X$。
将$X$传递给上层子模型作为下一个到达率$λₙ$
更新直到$|| λₙ₊₁ − λₙ || < δ$

我们从未观察到上述迭代未能收敛的情况。基于对缓存子模型的这种解决方案，包含缓存任务的LQN模型的整个解决过程在算法1中呈现，其中$f(·)$是为子模型$s$定制的求解器，它返回吞吐量、队列长度、响应时间和利用率。

4.3 Cache parameters and Markov process

上述用于分析缓存命中和未命中概率的缓存模型应用了基于列表的缓存[29]，[31]。基于列表的缓存由$h$个列表组成，形成树状拓扑结构，每个列表能容纳$m_l$个项目，$l = 1, 2, …, h$。总缓存容量为$m = ∑ {l=1} ^h m_l$，不超过总项目数 $n$。未被缓存的项目被安排在一个虚拟列表中，$l = 0$，其容量为 $m_0 = n − m$。由流$v$对列表$l$中项目$k$发出的请求率$λ{vk}(l) ≥ 0$遵循泊松到达过程，其中 $v=1,2,…,u, k=1,2,…,n$。

每个列表只能有一个父列表$p(l)$来交换项目，满足$p(p(···p(l)···)) = 0$，但对子列表的数量没有限制。没有子列表的列表被称为叶子列表。项目$k$在缓存命中后从当前列表$l$转移到列表$j$的概率是不均匀的，定义为访问概率$c_{vk}(l, j)$。对于此类基于列表的缓存的分析模型是基于马尔可夫过程的。在每个列表中，状态向量$s = [s(i, j)] ∈ [1, n]$代表在列表$j$的位置$i$中缓存的项目。应用的替换策略被建模为具有平衡概率$π(s)$的连续时间马尔可夫链（CTMC）。$π(s)$的乘积形式解决方案呈现为:
$$
\pi(S)=\frac{\prod_{j=0}^h\prod_{i=1}^{m_j}\gamma_s(i,j)j}{E(m)}
$$
其中$E(m)$是规范化常数, $γ{ij}$表示项目$i$访问列表$j$的访问因子，满足以下条件： $$ \gamma{ij}=\gamma_{ip(j)}\sum_{v=1}^u\lambda_{vi}(p(j))c_{vi}(p(j),j)
$$
马尔可夫分析模型的性能衡量标准是基于项目$k$在列表$j$中的边际概率定义的，表示为：
$$
\pi_{kl}(m)=m_l\gamma_{kl}\frac{E_k(m-1_l)}{E(m)}
$$
$π{k0}(m)$代表项目$k$的未命中比率，满足$π_k0(m) = E_k(m)/E(m)$，其中$E_k(m)$是当项目$k$不在模型中时的规范化常数。从边际概率出发，从流$v$请求项目$k$的未命中率可以表示为$M{vk}(m) = λ{vk}(0)π{k0}(m)(1 - c_{vk}(0, 0))$。因此，总的缓存未命中率是$M(m) = ∑{v,k} M{vk}(m)$。在此，我们关注单列表缓存，即$h = 1$，因为它们更为普遍，但我们的实现也通过上述公式支持 $h > 1$。

5. EXPERIMENTAL EVALUATION

在这一部分，我们首先评估使用分层队列网络（LQNs）来模拟作业调度和服务放置问题的优点。然后我们使用 Java 建模工具（JMT）[32]模拟基于队列Petri网（QPN）的模型，以验证广义 LQN 模型的准确性。最后，我们进行了广泛的模拟，使用真实世界的 Azure 跟踪数据来衡量广义 LQN 模型的性能。

5.1 Evaluation of LQNs for Edge Service Placement

我们首先将我们提出的方案与文献 [9] 中的方法进行比较，该方法提出了一个具有服务缓存的依赖任务卸载（ODT-SC）问题。ODT-SC 问题考虑的是具有确定性服务时间的确定性调度，而我们的方案关注的是具有随机服务时间的随机调度。此外，ODT-SC 问题的优化目标是最小化最大完工时间，即一个作业的开始时间与其执行时间之和，而我们的目标是最小化总响应时间。尽管假设有所不同，我们仍将这个基准视为与基于随机 LQN 的复杂边缘工作流建模的好处进行比较的合适对象。

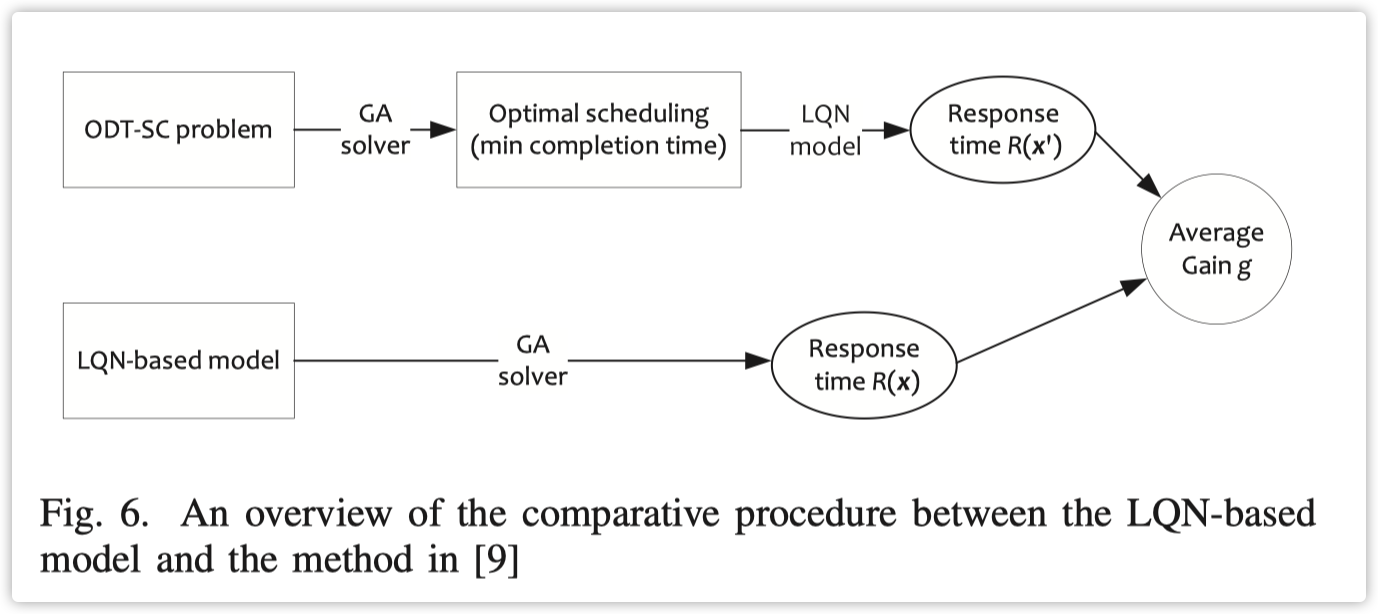
为了比较，我们将我们基于 LQN 模型中每个作业的平均服务时间设置为 [9] 中的执行时间。ODT-SC 问题的优化目标被重置为最小化总完成时间，即每个作业的完工时间之和。此外，[9] 中的方法将 ODT-SC 问题重新表述为凸规划以获得可行解。为了更通用，我们通过遗传算法（GA）解决 ODT-SC 问题，无需放松约束。两种方案的比较过程概述在图 6 中。

我们首先利用 GA 解决 ODT-SC 问题，获得每个作业的最优调度策略$x'$。然后将策略转换为 LQN 模型来计算总响应时间$R(x')$。每次迭代中对应于最小完成时间的响应时间被选为比较对象。同时，我们同样利用 GA 解决提出的基于 LQN 的模型，以寻找最小的总响应时间。最后，我们比较两个响应时间，以观察提出方法的平均增益 $g$，其表达式为：
$$
g=\frac{1}{I}\sum_{i=1}^I=\frac{||R_i(x')-R_i(x||}{R_i(x')}
$$
其中$I$是总的迭代次数

在每次迭代$ i = 1, . . . , I$中，为了减少估计误差，我们运行$Q$次 GA 求解器的复制来搜索最优解。在 GA 求解器的每次复制中，代数由 G 表示。ODT-SC 问题的设计变量维度为$2K$，其中前 $K$ 个元素和第二个$K$元素分别是每个作业的开始时间和调度决策。服务时间是确定性的，但在不同类型的服务中有所不同。而对于基于$LQN$的模型，设计变量的维度是每个作业的$K$个调度决策。每个作业类的服务时间被设置为指数分布或超指数分布，其平均值等于$ODT-SC$问题中的值。

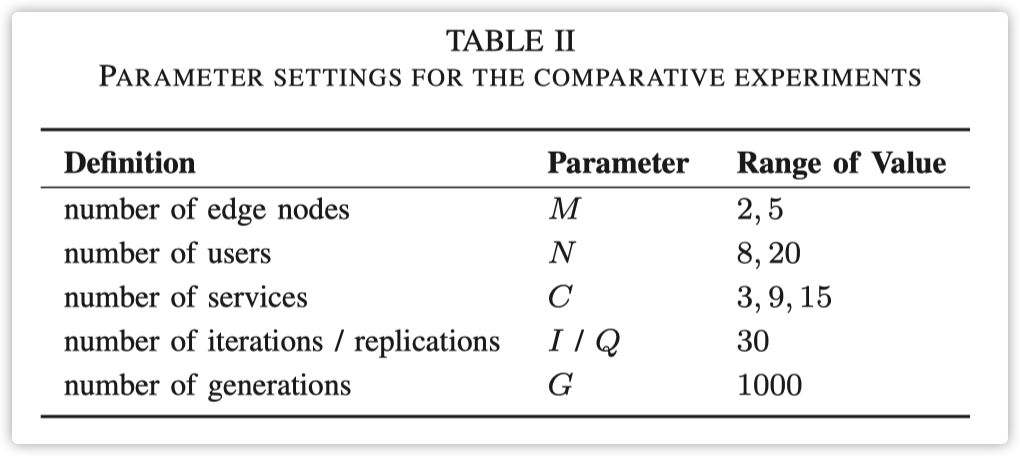
一系列实验被进行以分析在不同条件下的性能。不同参数的设置显示在表$II$中。服务时间的分布假设为指数分布或超指数分布。为了简单起见，用户工作流在实验中采用了多个服务的链式结构，但通过 LQNs 容易扩展到具有并行结构的情况。

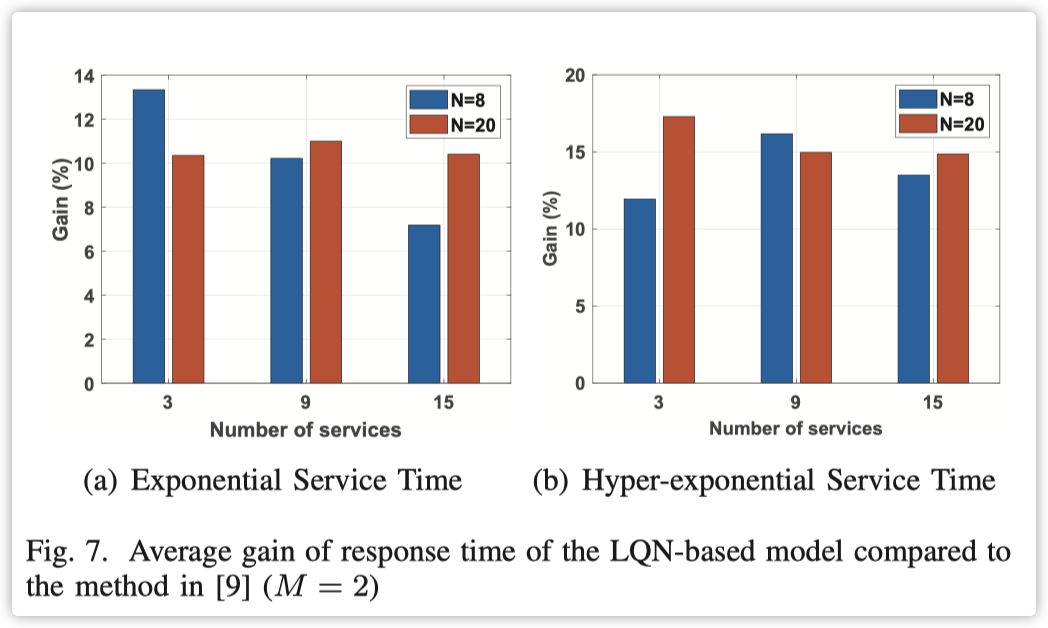
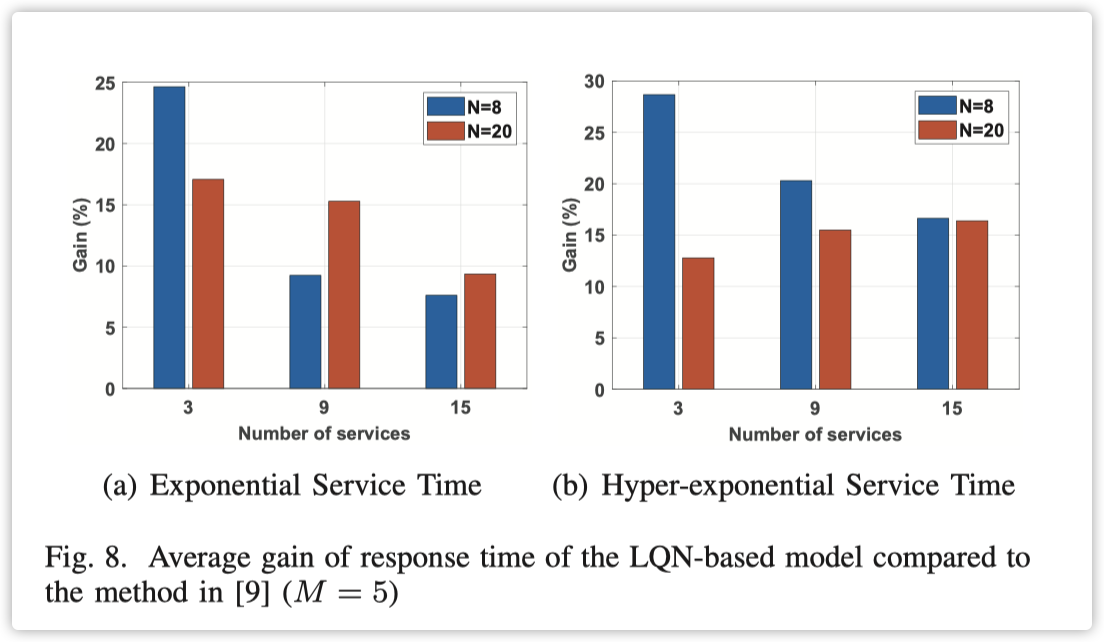
实验结果显示在图 7 和 8 中，可以看出使用 LQN 模型比 [9] 中的方法产生了更好的平均性能。当 $M = 2$ 时，总响应时间的增益最小为 7%，平均为 12%，最大为 17%。当 M = 5 时，总响应时间的增益最小为 7%，平均为 16%，最大为 28%。总体而言，平均增益随着边缘节点数量的增加而提高。我们的结果表明，与启发式地应用确定性调度相比，应用 LQNs 进行随机调度是有益的，即 ODT-SC 问题的解决方案。因此，使用 LQN 模型进行边缘缓存系统的进一步性能分析是有意义的。

5.2 Generalized LQN Model Validation

我们通过 JMT 验证了广义的 LQN 模型，JMT 支持带有图形用户界面的队列网络和 Petri 网的模拟。Petri 网允许我们将缓存中的替换策略建模为同步转换，这些转换会改变缓存槽。因此，通过模拟基于 QPN 的模型，我们可以准确估计带缓存的 LQN 的预期性能，并将其与我们在算法 1 中描述的基于 FPI 的实现进行比较。

我们考虑一个包含图 4 中所示模型上两层的验证模型。在上层，底层处理器 P1 采用处理器共享策略，用户数量由参考任务 RT1 的多重性表示。在下层，缓存任务的容量设置为 1，总共有 3 个项目。所有项目都遵循离散均匀分布，并采取 RR 策略。底层处理器 Pc 也采用处理器共享策略，这一层中的令牌数量由缓存任务的多重性表示。

验证模型被转换为 JMT 中的队列网络和 Petri 网的联合框架，如图 9 所示。作业首先起源于延迟节点，并存储在上层的位置。然后，利用 Petri 网转换，即等待输入位置中的令牌可用并在输出中发放给定数量的令牌，我们通过上层的 1 个作业和 1 个令牌，启用转换 2，将 1 个作业发放到下层。为了在下层确定缓存命中或未命中，我们将缓存的项目视为不同的作业类。因此，被发放的作业类可以根据概率分布在 ClassSwitch 1 节点切换到任何项目。基于存储在 Cache 和 OutOfCache 位置的项目的状态，转换 1 确定是否将命中或未命中的作业类发放到队列。在队列节点为命中或未命中的作业提供不同服务后，作业在 ClassSwitch 2 节点转换回原始作业类，并启用转换 3。最后，转换 3 发放 1 个作业到 Access Tokens 的位置，以及 1 个作业到延迟节点以迭代执行。

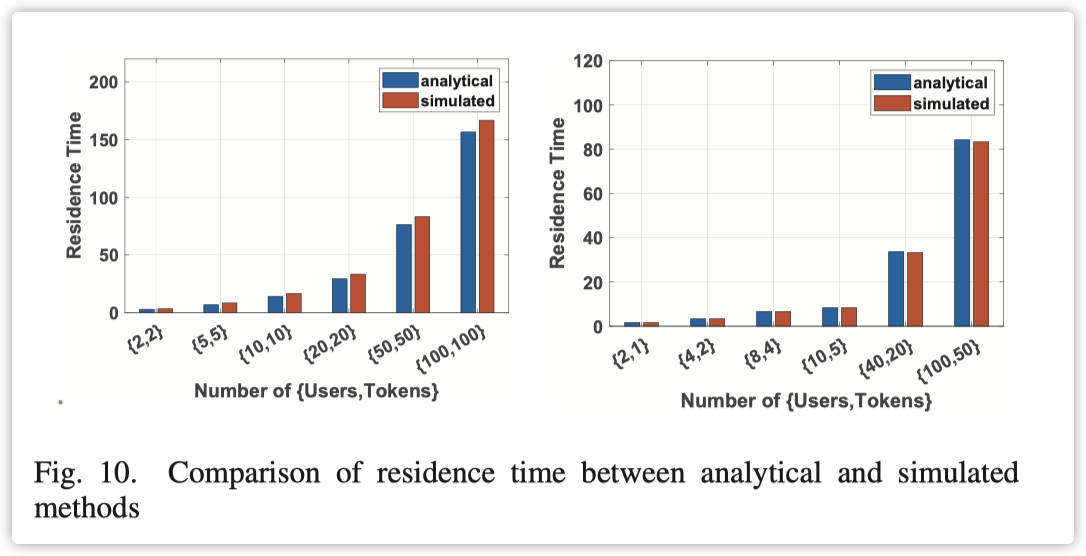
我们使用 JMT 模拟基于 QPN 的模型来验证分析模型。我们选择的性能指标是驻留时间，包括与响应时间相比的访问比率。结果表明，在不同用户和令牌数量组合下，分析模型和模拟模型之间的差异，如图 10 所示。结果表明，在所有情况下差异都可以忽略不计，这证明了广义 LQN 模型的高精度。

5.3 Evaluation of the JCSP Method

为了评估 JCSP 方法对实际工作负载的适用性，我们进行了基于跟踪的模拟，以证明该系统原则上适用于生产系统。该跟踪数据收集自 2019 年在 Azure Functions 上运行的一部分应用程序[33]。我们关注跟踪数据的一个随机子集，其中包含 34385 个应用程序 ID 和属于同一应用程序的相应无服务器函数 ID。跟踪数据还给出了每个函数的调用率、执行时间分布以及每个应用程序的内存使用分布。

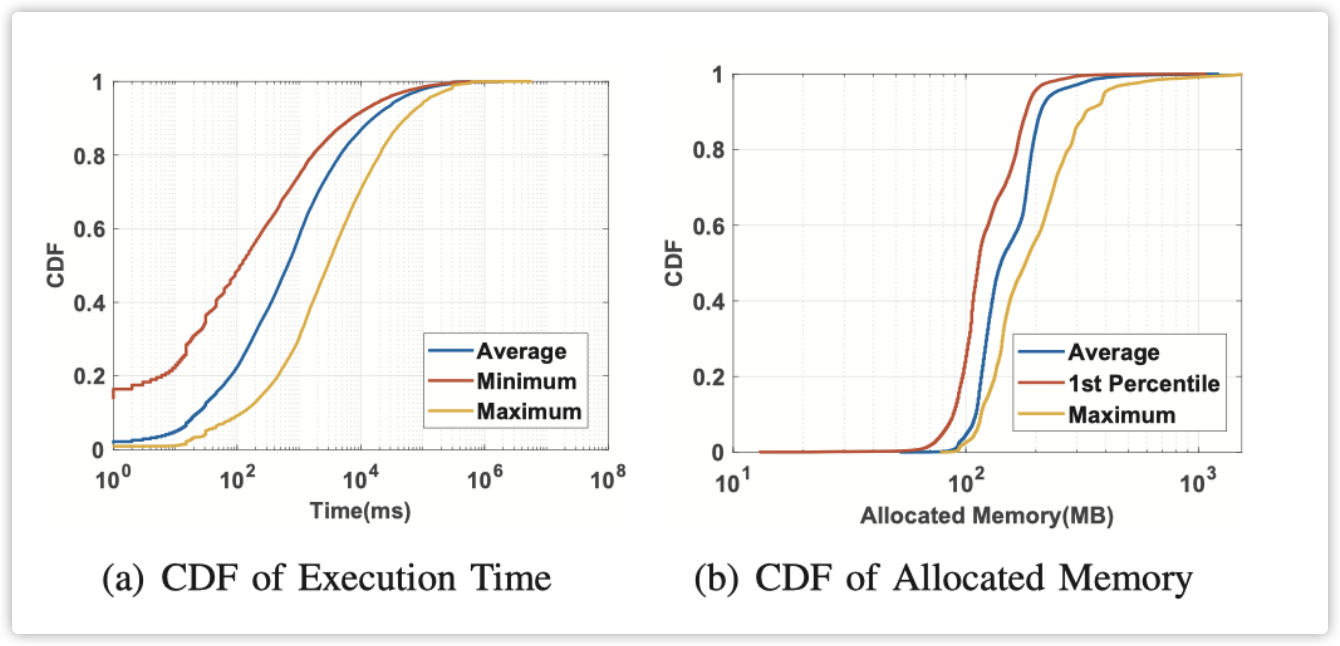
图 11(a) 显示了所有函数的最小、平均和最大执行时间的累积分布。我们可以看到，50% 的函数平均和最大执行时间少于 0.7 秒和 3 秒。90% 的函数最多执行 50 秒，95% 的函数平均执行时间少于 50 秒。图 11(b) 展示了所有应用程序的第 1 百分位、平均和最大虚拟内存预留的累积分布。每个应用程序调用一个或多个函数。我们可以观察到，99% 的应用程序平均消耗不超过 400MB，99% 的应用程序最多分配 1000MB。

为了模拟基于跟踪的数据，我们通过 LINE[10] 实现了带缓存的 LQN，以便于 JCSP 方法的实施。LINE 生成的广义 LQN 模型的一个示例如图 12 所示。深色六角星、粉色三角形、红色正方形和黄色三角形分别代表处理器、任务、条目和参考任务。边代表客户端-服务器关系。名称中包含 C 和 cloud 的点属于缓存和原始服务器。索引 h 和 m 分别指缓存命中和缓存未命中。非参考点的索引 i-j 表示节点 i 上的服务 j。

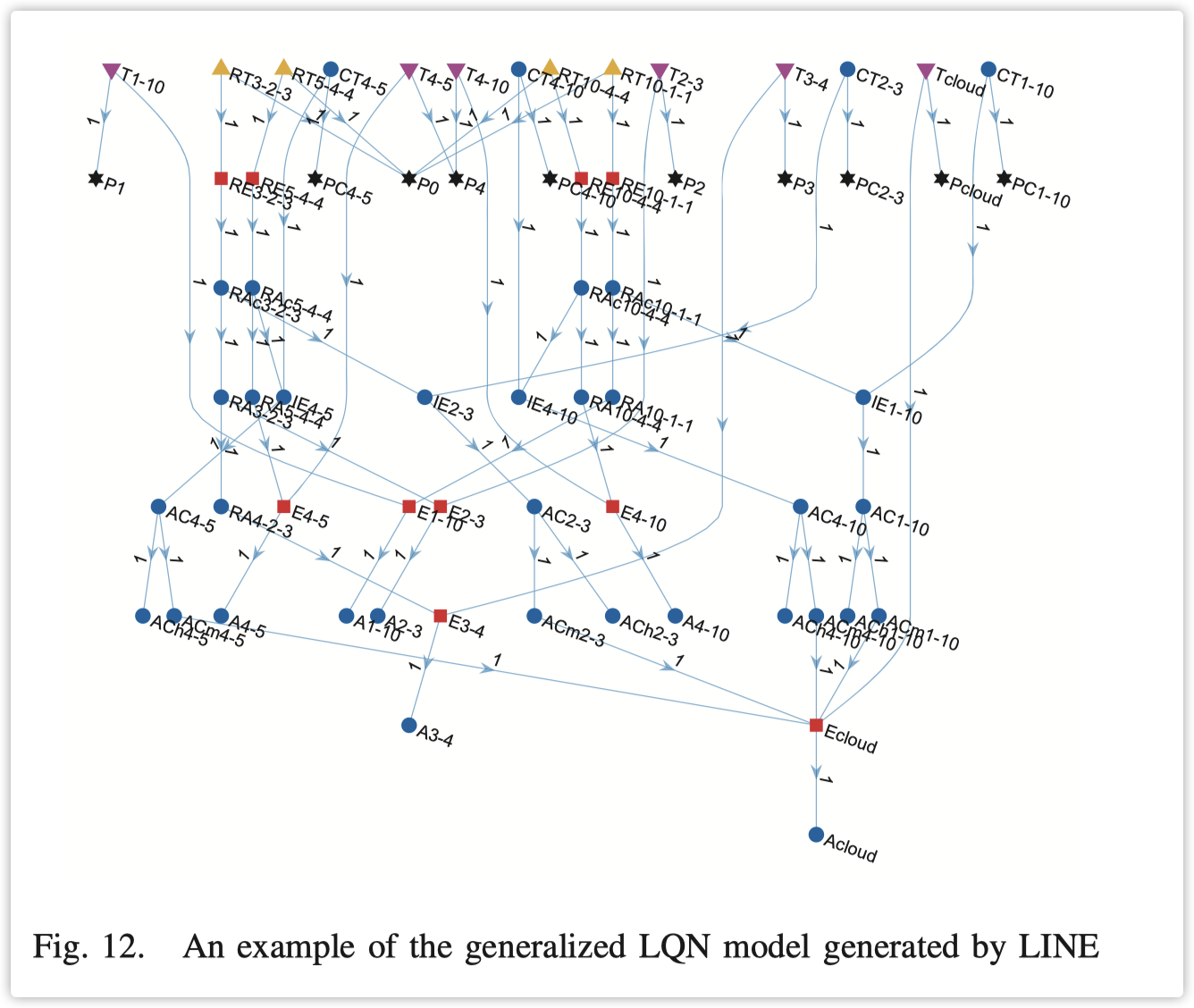
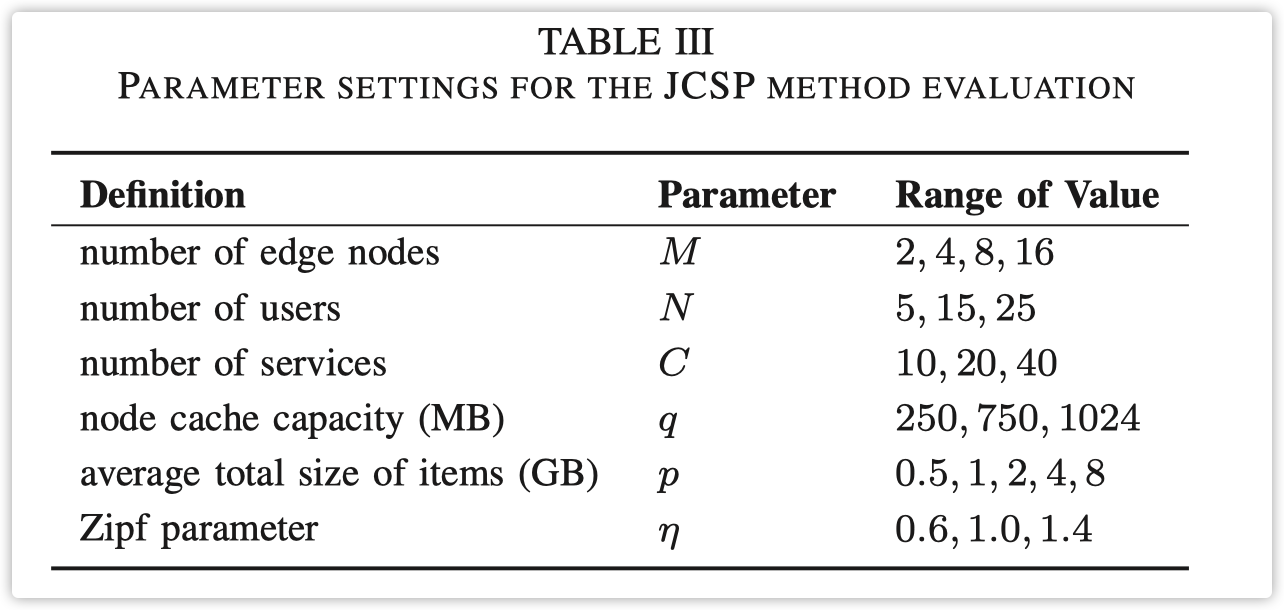
考虑缓存特性的参数设置在表 III 中呈现。每个节点的缓存容量 m 根据 Microsoft Azure[34] 提供的标准 Redis 缓存包进行配置。相应的缓存项目遵循 Zipf 分布，参数为 η，并假设大小相同，其总大小 n 与节点缓存容量成正比。表 III 中显示的与缓存相关的参数选择与早期工作[29]、[31]中的选择相同。与表 II 相比，边缘节点 d 和服务数量 s 分别扩大到 16 和 40。服务时间的分布假设为指数分布，平均值与从 Azure 跟踪数据收集的平均执行时间相同。用户数量考虑了 SBSs[35]的容量。对于每个用户，请求某项服务的概率由服务的调用率决定。

对于每组参数的组合，我们生成了 30 个具有不同随机种子的模型。在每个模型中，每个节点上的不同服务都添加了缓存任务，指定了每项服务的总项目大小和分配的缓存容量。服务容量之和等于节点缓存容量，这保证了每个边缘节点受限存储的最大利用率。我们采用总系统响应时间作为性能衡量，并将我们的 JCSP 方法与无缓存和全部预取的情况进行比较。无缓存方案不部署任何缓存模块，所有作业都需要等待从原始服务器获取所请求的内容后才能在本地处理。而全部预取方案表示每个边缘节点缓存所有项目，充分利用本地内存。

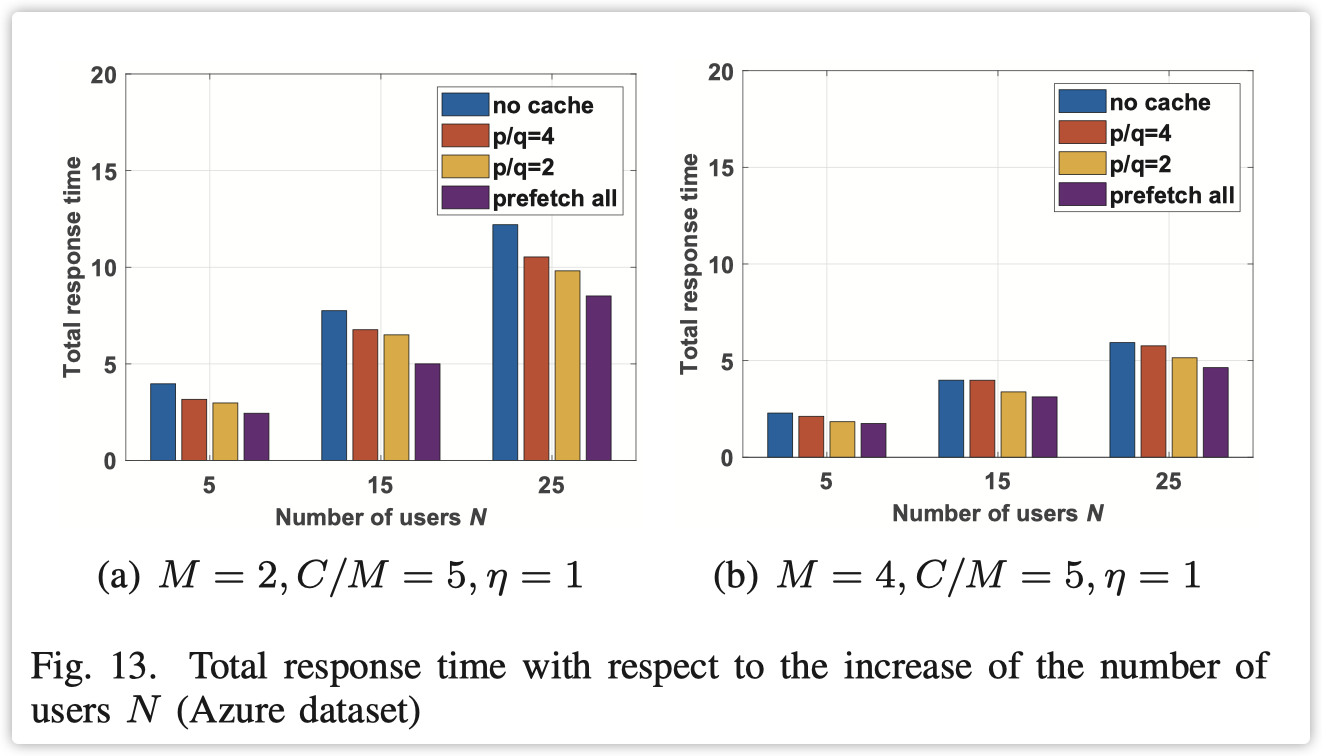
从图 13(a) 和 (b) 中，我们可以看到，在相同条件下，随着用户数量的增长，总响应时间增加，这归因于累积的排队时间。在相同用户数量下，无缓存方案作为基线显示出最高的响应时间，因为作业需要从原始服务器获取所需内容。相反，全部预取方案显示出最低的响应时间，但忽略了大量的内存消耗。与全部预取方案相比，尽管我们提出的 JCSP 方法显示出最多 35% 和 30% 的响应时间增加，但分别减少了 500MB 和 250MB 的内存使用。这是因为我们提出的系统基于不同边缘节点上的作业调度和服务部署策略优化了每项服务的缓存容量分配，实现了有限边缘资源的最大化利用。总体而言，当节点数量增加时，总响应时间显著下降，这得益于更多并发服务器带来的等待时间降低。

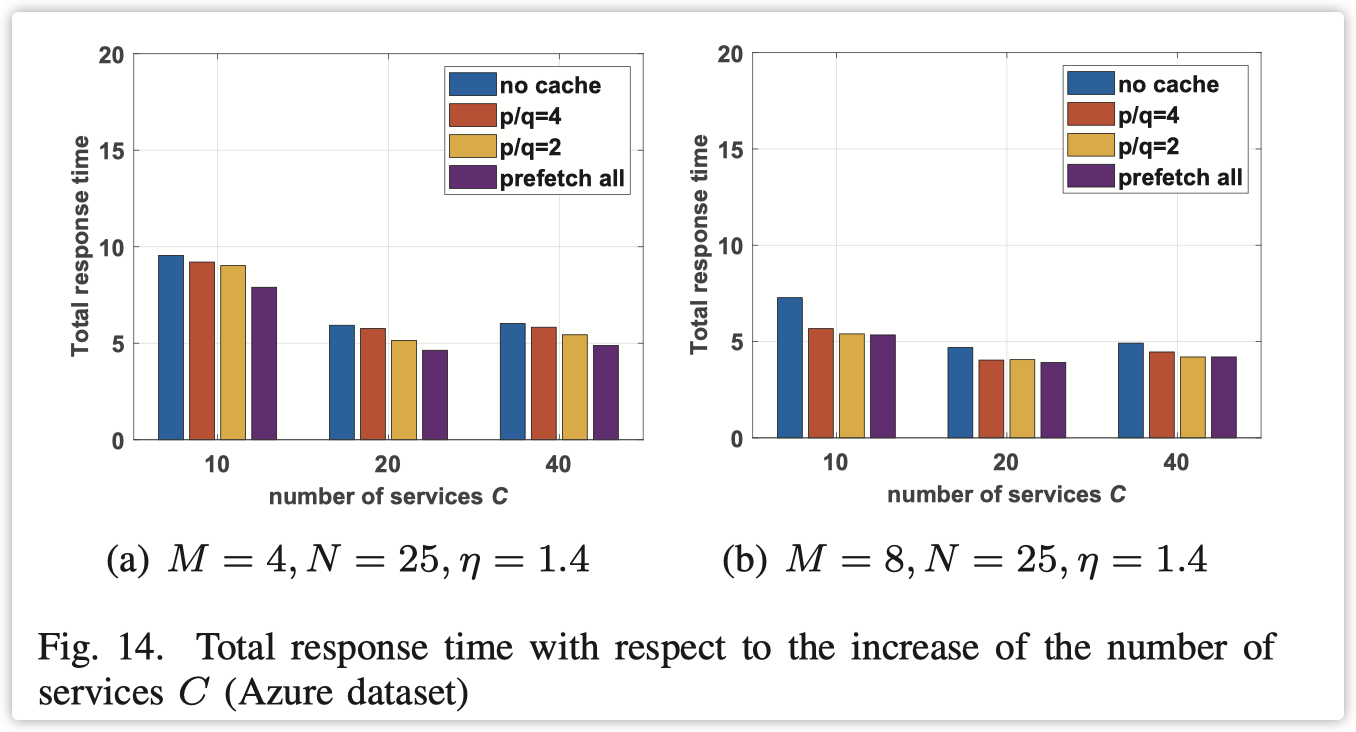
从图 14(a) 和 (b) 中，我们可以看到，随着服务数量的增长，总响应时间减少，但在 C 达到 20 后趋于稳定。第一阶段的下降趋势是服务数量少于用户数量的情况。在这种情况下，用户请求相同服务的可能性更高，导致相同服务器的排队时间更长。随着服务数量增长到等于或大于用户数量，调用相同服务的可能性减少，从而导致后期的平稳趋势。在相同服务数量下，我们提出的 JCSP 方法只看到最多 24% 和 14% 的响应时间增加，但与全部预取方案相比，内存使用量减少了 500MB 和 250MB。

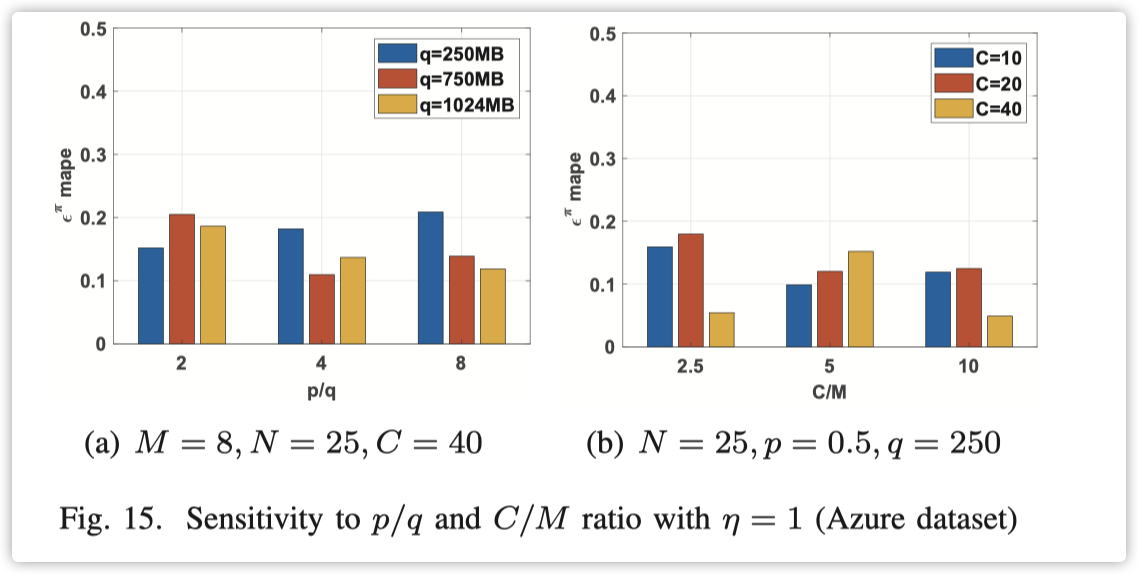
进一步地，我们分析了这些实验中$p/q$和$C/M$比率的敏感性。我们关注未命中率，并将性能指标定义为：
$$
\epsilon_{mape}^\pi=\frac{1}{Q}\frac{1}{M}\frac{1}{C}\sum_{k=1}^Q\sum_{j=1}^M\sum_{i=1}^C|1-\frac{\hat{\pi_{i,j}}}{\pi_{i,j}}|
$$
其中$\hat{\pi_{i,j}}$是对于节点$j$上服务$i$的预估未命中率。不包括用户在每个节点上没有请求的服务。从图 15(a) 我们可以看到，对于$p/q$比率，平均百分比误差$\epsilon_{mape}^\pi$大约在 0.1 到 0.2 之间。当节点的缓存容量较高时，随着总项目大小的增加，误差指标会降低。从图 15(b) 我们可以观察到，对于$C/M$ 比率，平均百分比误差$\epsilon_{mape}^\pi$大约在 0.05 到 0.15 之间。

5.4 Summary of Experimental Results

总的来说，随着用户数量的增加，与预取所有方案相比，JCSP方法显示出最多35%和30%的响应时间增加，但内存使用量减少了500MB和250MB。随着服务数量的增加，JCSP方法显示出最多24%和14%的响应时间增加，但与预取所有方案相比，内存使用量减少了500MB和250MB。这证明了我们提出的JCSP方法比简单的启发式边缘缓存资源分配策略更好。

关于执行JCSP方法的时间和空间要求，上述实验是在AMD EPYC 7302P 16核处理器上进行的。对于每次复制，内存使用和执行时间的估计不超过4.45MB和0.2秒，这反映了我们提出的JCSP方法适用于多种工作负载。

6. CONCLUSION AND FUTURE WORK

在本文中，我们提出了一种新颖的方法，用于联合分析边缘内容缓存和服务部署。我们首先使用LQN（Layered Queueing Networks，分层排队网络）共同建模了作业调度和服务部署过程。与文献[9]中的方法相比，基于LQN的模型显示出平均响应时间减少了16%。然后，我们通过加入缓存组件扩展了LQN模型，以便于JCSP（Joint Caching and Service Placement，联合缓存和服务部署）方法的实施。我们给出了一个分析模型，用于数值分析广义LQN模型。我们进一步通过JMT（Java Modeling Tools，Java建模工具）中基于QPN（Queueing Petri Nets，排队Petri网）的模型验证了广义LQN模型，并在LINE工具中实现了提出的集成缓存-排队模型。最后，我们进行了广泛的跟踪驱动模拟，以评估我们提出的JCSP方法在真实世界数据集上的性能，显示出在响应时间和内存消耗之间更好的权衡。

未来的工作可能会将验证扩展到一般的相位类型分布或涉及突发性的分布（例如，马尔可夫到达过程）。尽管我们的实现支持它们，但JCSP方法可以进一步用于理解将缓存分割成列表对端到端边缘工作流延迟的影响。