前两天写了一套真题,趁热来总结一波,虽然这套卷子比2004年的那套要更加基础一些,不过还是有一些值得总结的点。
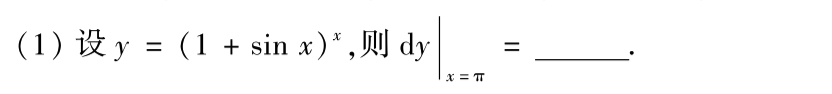
第一题就比较基础了,幂指函数,化e之后求导,然后代值即可

第二题也比较基础,我不太会用武忠祥的那个写成线性方程的形式,用的是算两次极限的方法,这道题其实还好,而且两次极限也更加稳健一点。
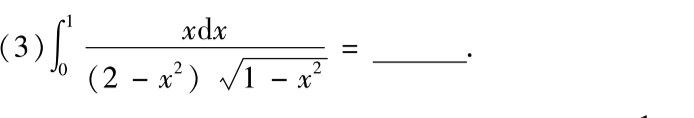
第三题,根号下的这种形式直接三角换元就可以了,然后就是三角函数的积分。
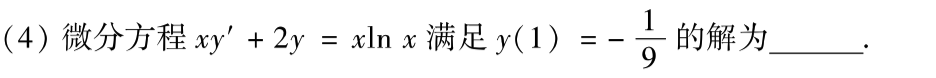
第四题也比较基础,两边同除x之后,一阶线性非其次,套公式就可以了。
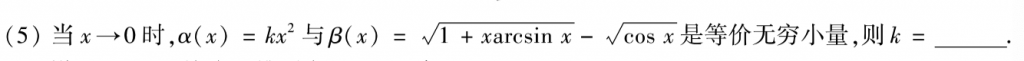
第五题的方法其实挺多的,可以用有理化,拉格朗日啥的,我用的是减一加一然后等价无穷小,这里补充一个公式:\(1-cos^{\alpha }x \sim \frac{\alpha}{2}x^{2}\),这里的\(\alpha\)就是1/2。
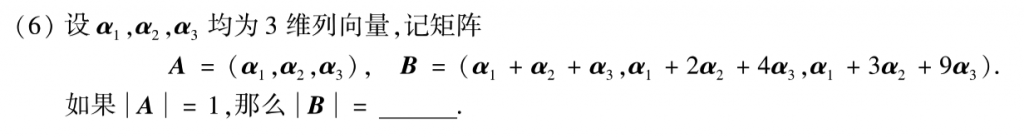
把B分解成A和另一个矩阵相乘(分块矩阵乘法),然后两边求行列式就好了。
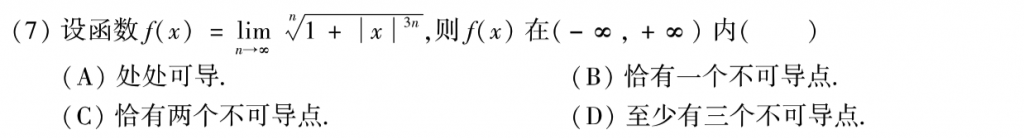
第七题做过好多次了,最简单的方法是画图然后分析,先看出来f(x)其实是偶函数,然后对x进行分类讨论,分为小于1和大于1的情况,把极限算出来,就可以得到函数了,然后根据函数的表达式画图即可。
另一种方法就是使用结论:(我当时做的时候居然没有看出来,结论还是研究的不够深,稍微变形一下成3n次方就识别不出来了qaq)
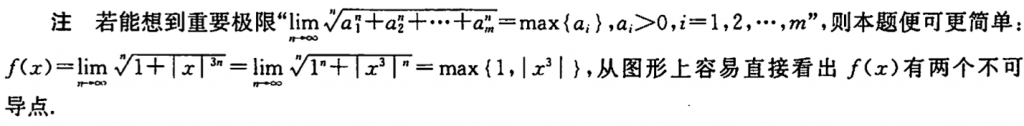

第八题也是一道非常经典的题,小细节就是如果一个函数是奇函数,那么它的所有原函数都是偶函数,但是如果一个函数是偶函数,只有一个愿函数是奇函数,因为奇函数要满足f(0)=0

第九题,写出法线方程,然后另y等于零就出来了。
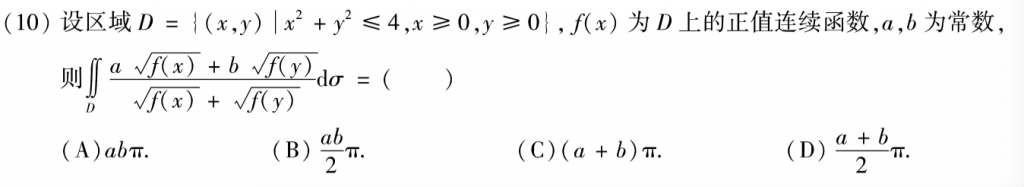
第十题也是一道非常经典的题,主要是要能意识到被积函数关于y=x对称,然后就可以把x和y对调,最后得到常数积分。典!

第十一题,这道题。。。我做的时候还以为我穿越到了去年的考场,这道题去年考了个差不多的,主要就是计算要细心,特别是这些正负号,如果粗心就很容易弄错。

第十二题,\(e^{\infty }\)分正负,典

这道题也是一道很好的题,先要把问题转换成这两个东西的线性无关判断:\(\alpha _1, \lambda _1\alpha _1+\lambda _2\alpha _2\),然后用定义,设k1k2,然后证明k1,k2全为零就好了,这一步还是比较难的,首先打开括弧,合并同类项,然后因为\(\alpha _1,\alpha _2\)线性无关,就可以得到他们前面的系数为零,得到一个方程组,根据这个方程组就可以得到k1和k2得0

第十四题也是经典题,做过好多遍的,PA=B,然后两边取伴随,那个P的伴随可以炸出一个负号来,而且到了右边,就变成了列变换。

第十五题,上面分开,下面换元,然后洛必达,求完导后,再用一个积分中值定理就出来了,如果这道题后面不用积分中值定理还挺麻烦的,凑导数定义啥的。

第十六题也是基础题,这套卷子唯一扣的细节问题就是在这,最后要用y表示x,我不知道为啥用x表示y了......
先把面积表示出来,然后两边求导就出来了。

第十七题也是基础题,先根据图像得到一些点的信息,比方说y''(3)之类的,然后反复使用分部积分就好了。

这题也基础,但是基础不一定简单,要对这种变量替换求导的东西很熟悉,有点类似那啥相关变化率。最后还走了一个微分方程,不错的。

又是经典例题,第一问直接走一个零点定理,唐迟都会:https://www.bilibili.com/video/BV1gW4y1a7ik
第二问就根据第一问,拉格朗日两次,然后相乘就出来了。

依旧经典,首先根据全微分的形式和f(1,1)可以求出z,具体的方法可以用全微分和偏积分,其实我比较擅长偏积分一些,全微分不太会用,但是这道题显然用全微分的方法更加简单。然后第二问就是求最大最小值,先在区域内部求,然后在边界上求,边界上求直接用拉格朗日也不难(我最讨厌的方法,算来算去还总容易漏接,麻烦)。
之前有人问过我为啥要分为区域内和边界上,实际上联系一元的最大最小值就可以知道,在区间内求导,然后和端点值比较,一样的道理。
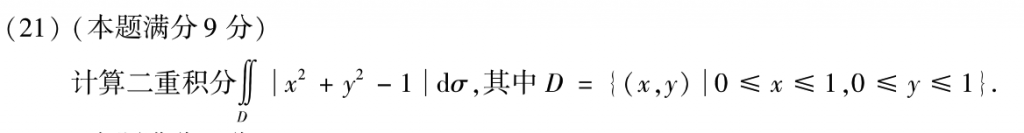
将积分区域分块,然后要注意扇形以外的那个区域的转化,用正方形减去扇形。
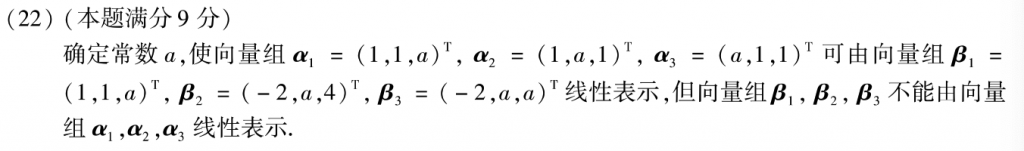
这道题比较基础的方法就是构造方程组,有解无解的判断,比较厉害点的方法就是用秩,用秩就很方便了。

这道题是一道非常好的题,主要难点在于分类,而且是r(A)=1的时候,,因为A是一个秩一矩阵,所以一定可以拆成一列乘一行,此时方程组和\(ax_1+bx_2+cx_3=0\)同解,然后因为A有一个解\((1, 2, 3)^{T}\),然后找到一个与这个解不相关的向量就好了,直接设\(x_3=0\)其实就可以满足了。







Comments NOTHING