这套卷子比较基础,除了微分方程的物理应用以外基本没有难度较大的题,但还是想在博客做个复盘,以后每做一套卷子,如果时间允许,我应该都会更新在博客。
填空题
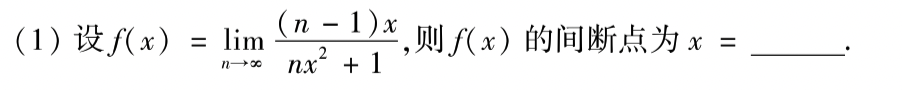
第一题比较基础,n趋向无穷,那么直接比较系数即可,极限算出来是1/x,那么间断点就是x=0

第二题难度也不大,既然曲线向上凸,那么就是二阶导小于零,对参数方程求个二阶导数,然后式子小于零,就可以将t的范围求出来。

第三题基础题,看到根号下的这种形式,想都不用想,直接换元,换元后被积函数为1,白给。
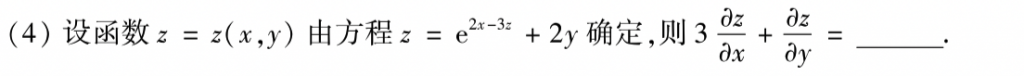
第四题也基础,怎么算都可以,我是讲这个式子全部移到了等号左边,然后用公式算的,也可以用微分形式不变形算微分。

第五题也比较简单,两边同除2x,然后就可以得到一个一阶线性的微分方程,求解即可。
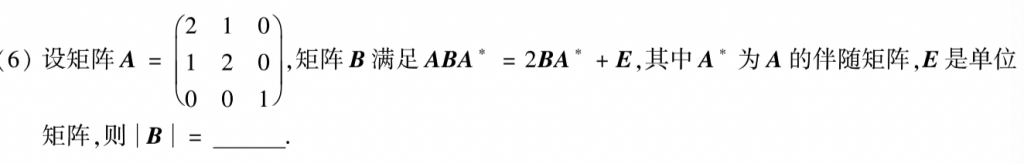
第六题也不难,我做这种伴随比较多的题一般都会用A来右乘,这样的话就可以把A*给消掉,变成行列式,然后再进行恒等变形计算就好操作了。

第七题用武忠祥的方法,n(m+1)直接秒了,cos那个当作0阶

第八题最快的方法是使用图像法,画一个抛物线,然后把小于零的部分翻上去,x=0那个点是尖点,那么就肯定是极值点,然后再观察凹凸情况就能判断是拐点。另外补充一句,其实一般的可导函数,一个点要么是极值点,要么是拐点,只有当在这点处的导数不存在的时候,就有可能出现一个点既是极值点,又是拐点的情况。详情参见660的161和162题。
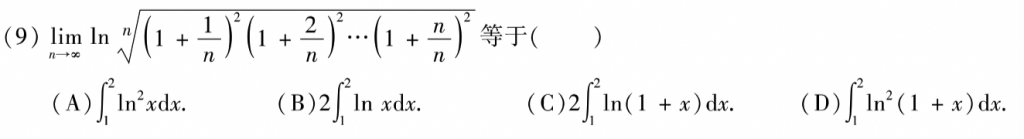
第九题把n次根号先拿到前面,然后ln相乘拆开,变成相加的,再利用定积分的定义,就可以把式子列出来,然后还需要进行一步换元的操作,才能得到答案。

第十题是一道很经典的题,在一个点处的导数值大于并不能推出领域内单调增,只能推出在这个左边的点都比它小,右边的点都比它大,至于左右两边各自的点的分布情况则是不清楚的,除非导数连续,才可以推单调性。详情可以参见660的第158题。
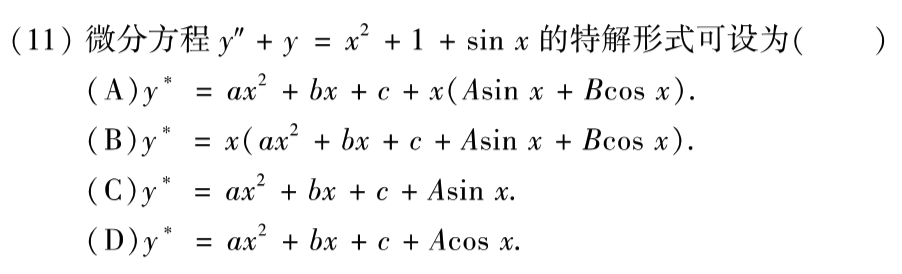
第十一题,直接求特征方程,然后将特解分成两部分,然后再根据非其次部分设特解即可,基础中的基础,没啥好说的。
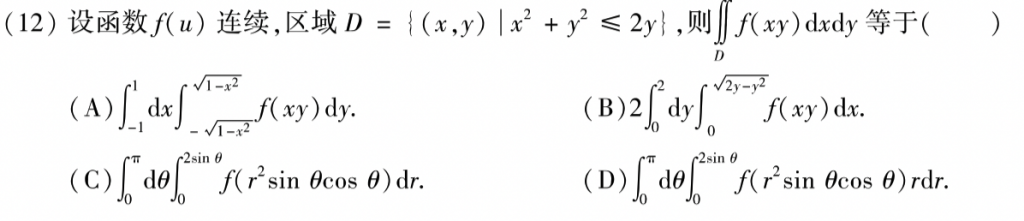
第十二题也是基础中的基础,,直接走一个D

第十三题跟着模拟就行了,要记住左乘初等矩阵是进行行变换,右乘是列变换,我总是容易忘...

第十四题,我一般搞这种就直接分块
$$
A\times B=(\alpha_1, \alpha_2,…,\alpha_n)\times (\beta _1,\beta _2,…,\beta _n)^{T} =\alpha _1\times \beta_1+\alpha _2\times \beta_2+…+\alpha _n\times \beta _n=0
$$
\(\alpha\)和\(\beta\)都是非零的,然后根据线性组合的定义,就能知道A的列向量和B的行向量线性相关
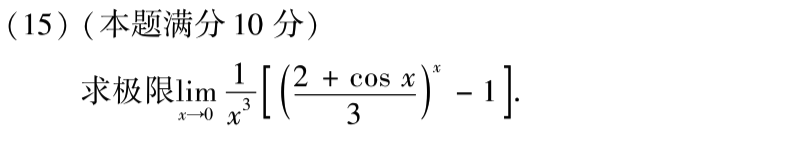
第十五题也是非常基础的题,但是我算的时候又又又粗心了,掉了个系数,血亏。

第十六题我一开始还卡了一会,主要是基础确实不太行,x的范围,f中括号的范围,傻傻分不清。因为题目说对于任意的x都有\(f(x)=kf(x+2)\),那么\(f(x-2)=kf(x)\)也是成立的,这个时候如果x的范围是从0到2的,而且x-2的范围就是-2到0,我在这里换了一个元,令\(t=x-2\),推出\(f(t)=k(2+t)\),然后带到题目给的f(x)里头就行了。
第二问就很简单了,分段函数,左导数=右导数就能建立关系,推出k

第十七题还是有些难度的,需要对换元的手法非常了解
中间用了一手\(u=t-\pi\)
$$
f(x+\pi)=\int_{x+\pi }^{x+\frac{3}{2}\pi} |sint|dt=\int_{x}^{x+\frac{1}{2}\pi} |sin(u+\pi )|du =\int_{x}^{x+\frac{1}{2}\pi }|sint|dt=f(x)
$$
第二问我也卡了一会,然后想到了第一问的结果表明f(x)是以\(\pi\)为周期的,因此只需要分析\((-\frac{\pi }{2},\frac{\pi }{2} )\)这段区间的最大最小值就可以了,主要就是求导数比较端点和极值点的大小,但是看了答案发现0到pi会更简单一些。

第十八题就比较简单了,套公式就完了,skip
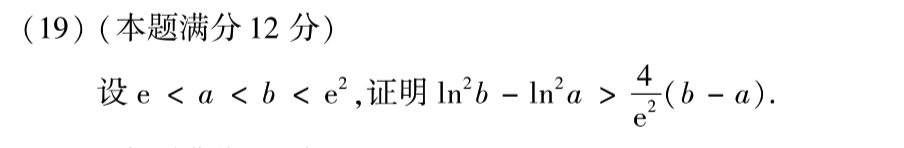
第十九题我是用的拉格朗日,令\(f(x)=ln^{2}x\),拉格朗日用完之后,需要对克赛进行放缩,所以我又令\(g(x)=\frac{lnx}{x}\),求导分析单调性,就可以完成放缩。

物理题,跳了跳了

送分题,没啥好说

也是基础题,系数行列式等于零,就可以求出a,然后算通解,当然,比较快的方法是直接化成阶梯形,然后秩小于4,也可以把a求出来,还可以顺便把通解给求了。

这道题也不难,但是容易出错,这道题应该是我第二次做了,印象比较深刻,因为我第一次做的时候就掉了一种情况,算出来有一个因子是\(\lambda-2\),所以要么\(\lambda=2\)是二重根,要么后面那个东西是一个完全平方,这就是两种情况,然后对于每一种情况,具体分析是否可以相似对角化。
ok,复盘结束。







Comments 4 条评论
xd你本科哪的,为什么要执着于暨大呢?22408有跟好的选择
@晨Cyan 坐标武汉,广州+211可选太少了,就暨大和华师,我更喜欢暨大一些。另外就是在我复习迷茫的时候,遇到了许多暨大的学长,他们的帮助就如雪中送炭,所以我想今年再头铁一年hhh

@vsbf 科软—22408去年难度降下来点,可以实习的。你可以知乎搜一下,我觉得你可以冲这个,研究生了地域没那么重要,科大名头还好使一点。我会关注你的,加油
@晨Cyan 科软感觉不太好把握,一年炸一年不炸的,今年感觉也不好说hhh。感谢关注,我会加油的!