都说数据结构是算法的加速剂,这句话在优先队列的身上得到了很好的体现。
我们看名字就知道,优先队列肯定和队列是同一个家族的,只不过不同的是,队列的出队是按照位置来的,每次都是前面的第一个元素出队。而优先队列的出队顺序是按照优先级来的,在有些情况下,我们需要进行大量的取集合中最大或最小值的操作,那么就可以用优先队列来完成。优先队列支持插入和取最大或最小值操作并将其删除。

优先队列是由堆来实现的,堆是一种二叉树:儿子的值一定不小于/不大于爸爸的值,堆的例子:(挑战程序设计上的,这里的堆是小顶堆 ,就是取最小值很快)
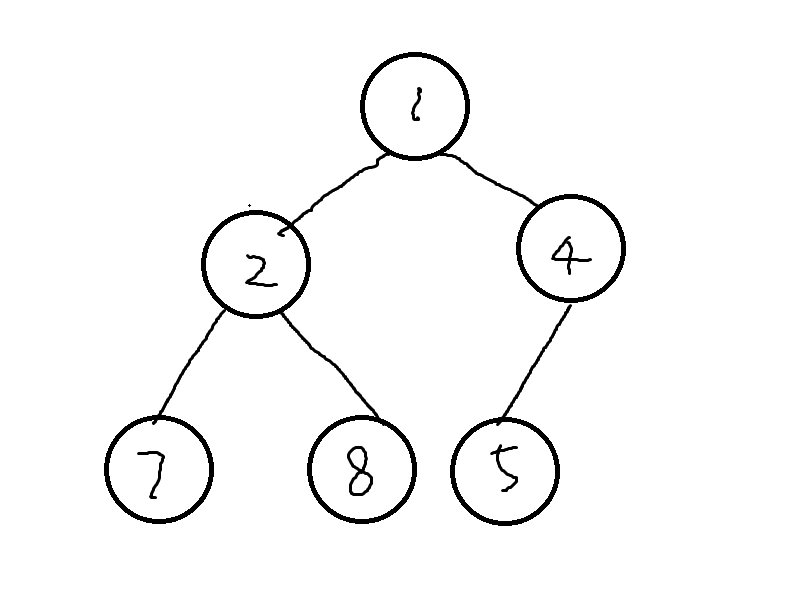
heap取最大值或最小值的速度特别快,看图就可以知道,最小值就是top的位置,所以其取最大值/最小值时间复杂度低至O(1)
| 实现 | 插入 | 删除 | 寻找最值 |
| 无序数组 | O(1) | O(n) | O(n) |
| 无序列表 | O(1) | O(n) | O(n) |
| 有序数组 | O(n) | O(1) | O(1) |
| 有序列表 | O(n) | O(1) | O(1) |
| 二叉搜索树 | O(log n) | O(log n) | O(lon g) |
| 平衡二叉搜索树 | O(log n) | O(log n) | O(log n) |
| 堆 | O(log n) | O(log n) | O(1) |
在c++中使用优先队列:
在实际做题的过程中,并不需要我们实现堆,C++中的stl已经封装好了,我们只需要会用就行,这样可以帮助我们把更多的精力放在算法的设计上。
首先需要引用头文件: include<queue>
我们可以使用如下操作:
| name.empty() | 判断队列是否为空,为空返回1 |
| name.size() | 返回队列中的元素个数 |
| name.pop() | 删除堆顶,不返回值,类似dequeue |
| name.top() | 取堆顶的值,不删除 |
| name.push(Elem) | 插入elem到队列中,类似enqueue |
由于优先级队列默认为高优先级,而有时候我们想自定义其优先级。priority_queue的模板带三个参数:priority_queue<Type, Container, Function>,分别是元素类型,存储的容器和比较的方式,注意这里的container不能用list,最好用vector。
使用priority_queue需要注意的:
1、由于priority_queue默认为高优先级,所以如果我们省略后面两个参数:priority_queue<Type>,则就是大顶堆。
2、如果要使用小顶堆,则需要将模板的三个参数都带进去,STL里面定义了仿函数greater< >,使用这个可以声明小顶堆:priority_queue<int, vector, greater<int>>。
3、如果是自定义,则需要重载operator<来实现:
#include <iostream>
#include <queue>
using namespace std;
struct Node{
int x, y;
Node( int a= 0, int b= 0 ):
x(a), y(b) {}
};
bool operator<( Node a, Node b ){//升序
if( a.x== b.x ) return a.y> b.y;
return a.x> b.x;
}
int main(){
priority_queue<Node> q;
for( int i= 0; i< 10; ++i )
q.push( Node( rand(), rand() ) ); //构造函数
while( !q.empty() ){
cout << q.top().x << ' ' << q.top().y << endl;
q.pop();
}
getchar();
return 0;
}
4、自定义cmp
struct cmp{
bool operator() ( Node a, Node b ){
if( a.x== b.x ) return a.y> b.y;
return a.x> b.x; }
};
priority_queue<int, vector<int>, cmp>
优先级队列是一种特别重要的数据结构,在许多算法中都可以看到它的影子,比如哈夫曼编码、 Dijkstra算法、Prim算法、寻找第k个最小元素等等...所以需要好好掌握。
3.27更新手写堆:
#include<iostream>
#include<algorithm>
#define LE(X) ((X) << 1)
#define RT(X) ((X) << 1 | 1)
#define DAD(X) ((X) >> 1)
using namespace std;
struct heap {
int w[400005];
int tot;
int top() {
return w[1];
}
void modify(int x) {
if(x == 1)
return;
if(w[x] > w[DAD(x)]) {
swap(w[x] , w[DAD(x)]);
modify(DAD(x));
}
}
void push(int key) {
w[++tot] = key;
modify(tot);
}
void repair(int x) {
int tar = w[LE(x)] > w[RT(x)] ? LE(x) : RT(x);
if(w[x] < w[tar]) {
swap(w[x] , w[tar]);
repair(tar);
}
}
void pop() {
swap(w[1] , w[tot]);
w[tot--] = 0;
repair(1);
}
};
int main() {
heap hp;
hp.push(1);
hp.push(2);
cout << hp.top() << endl;
hp.pop();
cout << hp.top() << endl;
return 0;
}







Comments NOTHING