查找,是数据结构中一个特别重要的点,这篇文章我主要说的是二分查找
在有序数组中查找key,一般使用遍历这种方法可以简单粗暴的查找到我们所需要的元素,但是我们可以有更好的办法!
W6%7DSTL.png)
首先我们有三个变量low,middle和high,它们分别指向的是数组的第一个元素,中间的元素和数组的最后一个元素
首先取middle = (0 + 9) / 2 = 4, 第一次查找的时候发现key<middle,那就说明我们所需要查找的关键字在数组的左半边,所以我们这个时候将high = middle - 1 = 3(为什么不是4 而是要往左边移一位需要好好考虑),而middle = (0 + 3) / 2 = 1,状态就如下图所示
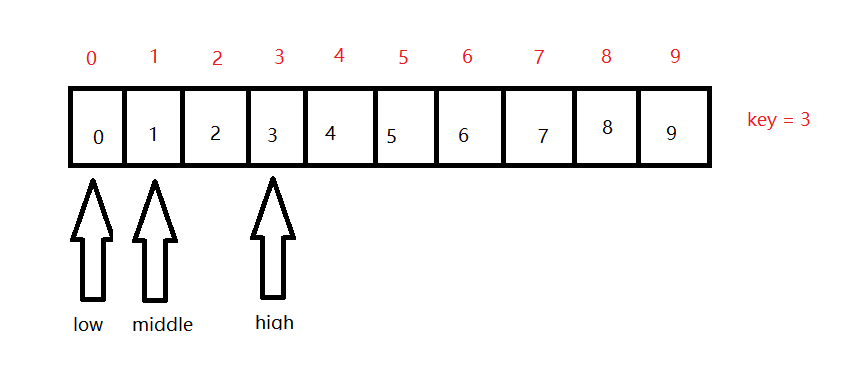
第二次查找的时,key>middle,说明是在当前区间的右边,所以我们只需要将low = middle + 1 = 2,middle = (2 + 3) / 2 = 2,状态如下图所示:
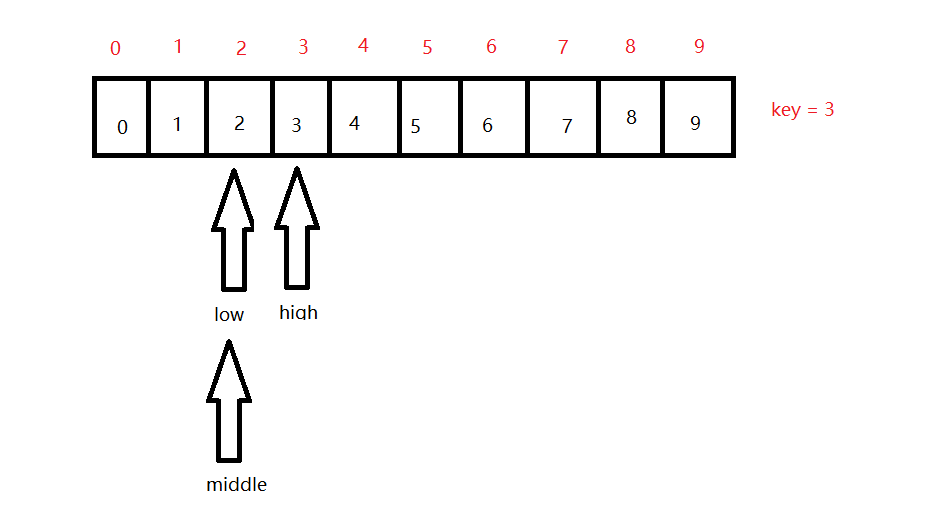
第三次查找时,key>middle,说明在当前区间的右边,所以我们同样只需将low = middle + 1 = 3,middle = (3 + 3) / 2 = 3,所以目前的状态如下:
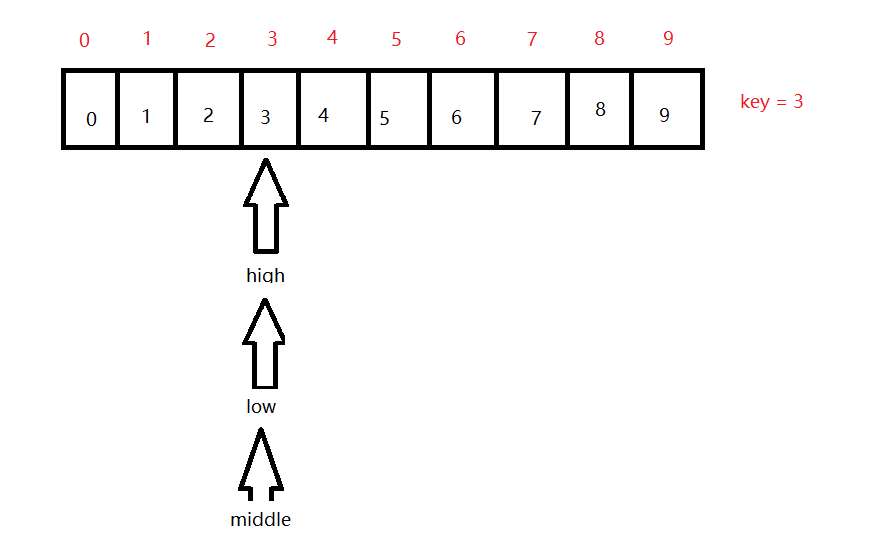
现在low、high和middle都指向了3,middle = key 成功命中元素,完成!
没有找到元素的情况和上面的推到类似!这里由于篇幅的原因就不多讲,可以自己手推一下(实践是检验真理的唯一标准)。
总结:循环的条件:low<= high;如果key在区间左侧:high = middle - 1;如果key在区间右侧:low = middle + 1。
代码描述:
有了上述的原理分析之后,再阅读代码应该不太困难,代码有不懂的地方欢迎在评论区留言。
#include<iostream>
using namespace std;
template <typename T> //使用c++的模板
int binary_search_array(const T & key , const T data[] , int N)
{
if(N < 0)
return -1;
int low = 0;
int high = N - 1; //high是真实存在的位置,也就是数组的最后一个元素
while (low <= high)
{
int middle = low + (high - low) / 2; //若low + high是一个非常大的数,会造成溢出,所以以这种形式写
if(key < data[middle])
high = middle - 1;
else if(data[middle] < key) //使用模板,所以只用了小于号,以后不需要再另外重载大于号
low = middle + 1;
else
return middle;
}
return -1;
}
int main()
{
int a[5] = {1 , 2 , 3 , 4 , 5};
cout << binary_search_array(2 , a , 5) << endl; //查找2,从第一个元素开始,一共有5个元素
cout << binary_search_array(0 , a , 5) << endl; //查找0,从第一个元素开始,一共有5个元素
cout << binary_search_array(2 , a + 2 , 3) << endl; //查找2,从第三个元素开始,一共3个元素
cout << binary_search_array(0 , a , 0) << endl; //查找2, 从第一个元素开始,一共0个元素
}







Comments 1 条评论
暖贴,fxp到此一游