这张试卷是今天上午做的,终于把李永乐的试卷刷完了,这周的剩下几天就把前段时间所做的真题和模拟题再看一遍,查漏补缺,准备好做下一阶段的试卷,比如李艳芳的三套卷、李林的六套卷,张宇的八套卷和四套卷等等。
客观评价李永乐的这张卷子,我感觉选填难度不大,终于做全对了,但是大题我感觉有些难度,总的来说质量还可以。
现在开始复盘

第一题是比较简单的,用导数定义就好了
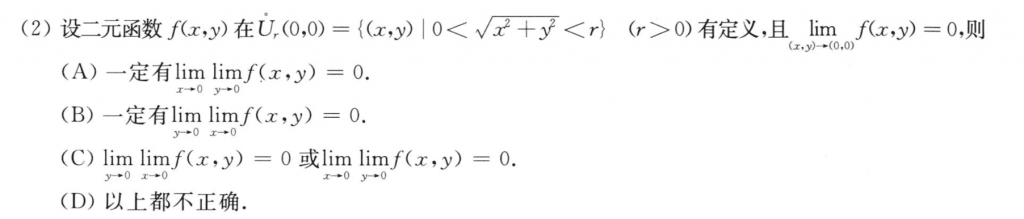
第二题也不难,同时取极限和先后取极限不是一个东西,所以就直接走D了
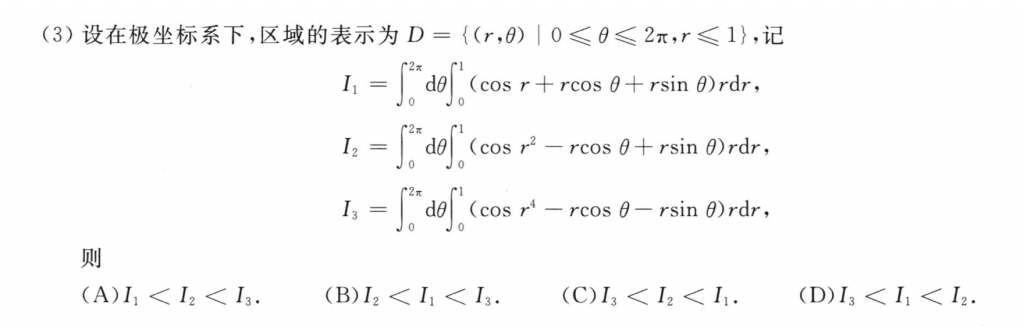
这道题也不难,$sin$和$cos$的奇次方在一个周期($2\pi$)上的积分是零,如果是偶函数的话,就是$[0, \frac{\pi}{2}]$的四倍,所以现在就把问题转化成了比较$cosr, cosr^2, cosr^4$的大小。
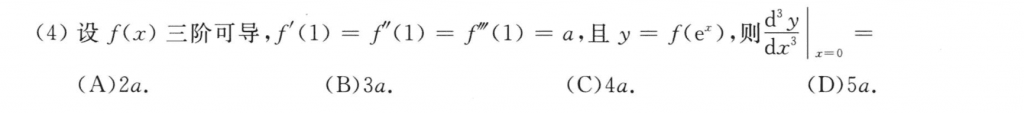
复合函数求导,基本题
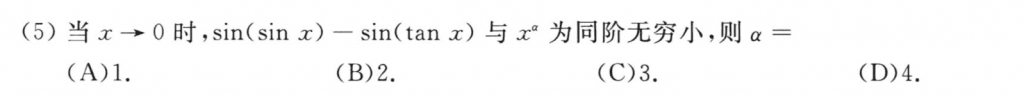
这道题我算都没算就选了C,因为这个函数是奇函数,那么只能选A或者C,A铁定是不可能的,那么就只能选C了。

这道题也不难,只需要考虑$f(x)|sinx|$,武忠祥上课讲过这种形式判断是否可导就看前面$f(0)$是否为零,而且是充要条件。

主要是要知道圆的体积的公式$\frac{4}{3}\pi R^3$,球壳的体积就是外面大球的体积减去里面小球的体积,表达式列出来以后,再用复合函数的求导法就可以求出来了。

首先根据基础解系里头的向量个数可以把A的秩求出来,然后把A按列分块以后再把这两个解带进去就可以得到$\alpha$之间的关系,然后判断就好了,其实很显然的选项是C,根据$\alpha$之间的关系我们可以知道$\alpha_1$和$\alpha_3$是线性相关的,所以如果$\alpha_4$也可以由这俩表示,那么最后的秩就只有1了。

A经过初等行变换可以变成B,那么就存在一个可逆矩阵P,满足$PA = B$,根据这个式子就可以知道B的列可以由P的列线性表示,B的行可以由A线性表示,所以B肯定是对的,又因为P是可逆矩阵,那么$R(PA) = R(A) = R(B)$,根据这个就可以推CD正确。

合同,只需要正负惯性指数相同就好了。

$1^\infty$换皮,括号里头加一减一,然后用三部曲就可以推出来了。
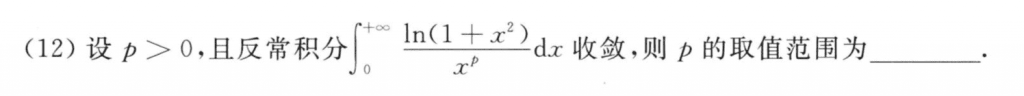
趋向零等价变换再判断,趋向无穷无视ln就好了

裸的二重积分,交换次序老朋友
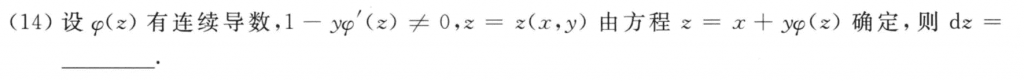
基本题

把x看成函数,y看成自变量,就好了。
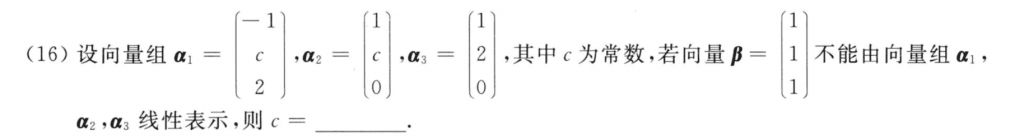
$\beta$不能由$\alpha_1, \alpha_2, \alpha_3$线性表示,那么对应方程组无解,作初等变换把c确定就好。

这道题感觉还是有点东西的,我想了好久,换了元以后把$f(x)$在$x = 0$泰勒展开然后再算,搞的还是比较繁琐的,答案这个操作就比较科学了,后面加项减项,然后用了积分中值定理,正好$ln(1+x) - x$可以合并,然后凑导数定义,行云流水的操作,值得学习。

这道题我感觉怪怪的,第一问肯定没问题,主要是第二问这个$\varphi(t)$,我还以为是个新函数,想了半天,结果发现就是第一问的$\varphi$啊,离谱。
第三问就比较简单了,第一问求了齐次的通解,第二问求了非齐次的特解,结合一下就ok了。
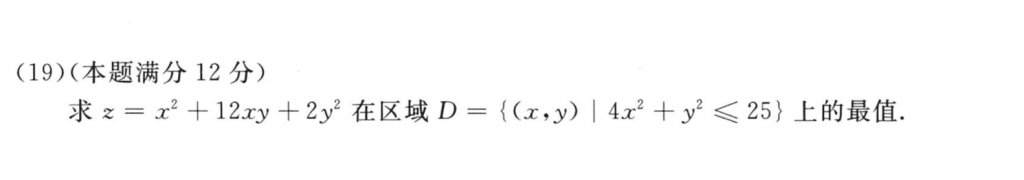
主要是算拉格朗日方程的时候有些麻烦,可以用齐次方程有非零解,系数行列式得零,把$\lambda$算出来,算出来有两个,分别带到式子里面求驻点就好,虽然说的比较简单,但是计算还是有点麻烦的。

这道题第一问我做错了,主要是方程式子出了点bug,如果不按答案的那种方法,对y积分的话,式子应该是这样的:$$2\times 2\pi\int_{b-a}^{b+a} y\sqrt{1+x'^2}dy$$
当然也可以把式子列出来以后用古尔丁定理一步到位:旋转体的侧面积等于$2\pi \times S \times L$,其中的S是旋转区域的周长,L是形心坐标到转轴的距离,那么也就是$2\pi \times 2\pi a \times b = 4\pi^2ab$
第二问就比较简单了,把质量面密度二重积分一下就行。

这道题前两问都不难,第三问是真想不出来。。

这道题可以用配方法,也可以用正交变换的方法,其实这种可逆线性变换一般来说标准的方法是配方法,但由于正交变换的方法对我们来说比较熟悉,不容易出错。另外就是有的题会卡特征值,让特征值的计算非常麻烦,或者按照常规的方法根本就算不出特征值,那么这个时候就只能选正交变换了。
复盘结束,李永乐的六套卷副本over,感觉这六套题还是很有水平的,以前总是听说李永乐的卷子比较拉胯,但是今年的变化还挺大,几个模拟卷交流群里的同学都觉得还不错,我也觉得很棒,推荐刷!







Comments NOTHING