2021李艳芳三套卷复盘&总结

今天做了一套芳芳去年的三套卷，在博客复盘一下，方便日后复习，也可以和大家交流，感觉模拟卷有人交流的话效果更棒，数一数二数三的试卷+解析全套电子版：

链接：https://pan.baidu.com/s/1szwt5e8qrWNYpVo9_VQ4_w
提取码：6666

芳芳今年的试卷和去年的试卷基本没有重题，而《三套卷》作为去年质量最高的模拟卷，今年肯定也是非常值得做的（去年的卷子，今年居然卖断货了。。）。我今天上午做了一套，质量是真的高，和我做真题的感觉基本一样，当然，还是比真题难的，但是也确实是真题的难法

updata：11-09
三套卷做完了，分数情况如下：

题型	第一套	第二套	第三套
选择填空	70	60	70
解答题	48	27	37
总分	118	87	107

第一套（公式显示不出来刷新下）

分数大概在110-120之间，我自己打的是118，算错了的题给了一点过程分。其中选填各错一道，18题积分计算失误，19题条件看错导致整道题做错，21题第二问条件转化不会，没做出来。

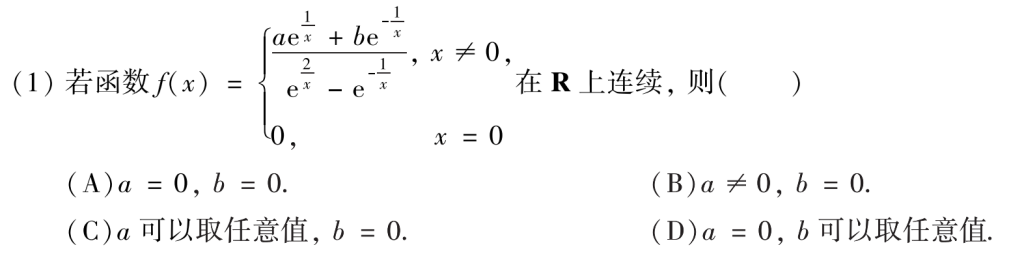
第一题是很常规的题，唯一的坑点在于\(e^{\infty}\)需要分正无穷和负无穷，这个点是武老师反复强调过的，基本没什么问题。

第二题主要就是考察线性主部的概念，我第一次接触是在张宇的1000题，当时比较懵逼，第二次接触是在做真题的过程中，这是第三次接触了，对y求导之后把零带进去，左边就是\(y'\left( 0 \right) =\frac{\Delta y}{\Delta x}\left| _{x\rightarrow 0} \right.\)这样就用到了线性主部的条件。

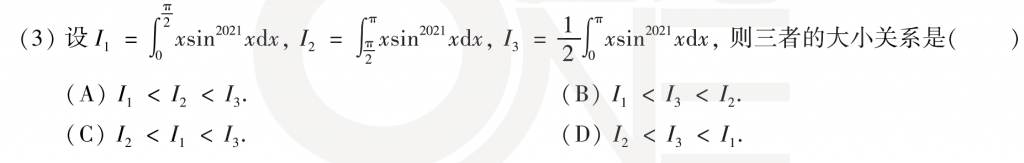
第三题答案是纯计算的方式，把\(I_2\)做变量替换\(t=\pi -x\)之后与\(I_1\)进行比较，我直接通过武老师讲过的几何的方法看出\(I_1\)<\(I_2\)，因为sin两项关于\(\frac{\pi}{2}\)对称，积分出来肯定是相等的，但是x明显在后面的区间内更大，所以推出\(I_1\)<\(I_2\)，然后\(I_1\)+\(I_2\)=2\(I_3\)，再把\(I_1\)放大到\(I_2\)，就能推出最终的结果。

第四题其实很常规，用x分区间之后求导就可以了，计算上可能得稍微注意点，容易出错，我算了两遍。

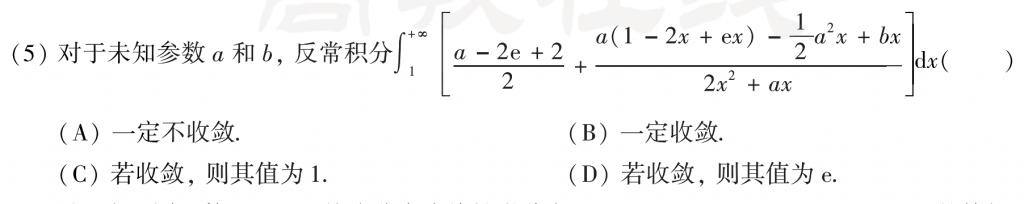
第五题我做错了，因为被这个式子给吓到了，不知道怎么处理，就像武老师说的那样，胆子不够大，其实直接通分就好了，简单粗暴，通分之后分子有常数项、一次项和二次项，，要保证反常积分收敛(p>1)，就需要一次项二次项前面的系数为零，然后就可以把反常积分求出来了。

第六题其实也不难，我是直接把每一个选项的小括弧打开，然后根据\(C_1, C_2\)来重新合并同类项，就可以很清楚的看到解的结构了，唯一的难点就在于判断\(\frac{y_2-y_3}{y_1-y_3}\)不为常数，我是直接猜的，然后猜对了hh。

第七题直接用武老师讲的结论就可以直接秒杀，首先分子四次分母二次，极限一般为0，就能推连续，不放心的话放缩也可以，也比较简单。判断偏导的时候，也能加速，比如对x求偏导，可以先把y=0带进去，这样的话式子恒为0，求导肯定为0，得到两个偏导都为0。可微的话，其实就是把分母变成3/2次方，分子次数还是高，所以直接秒杀。（当然，有风险，看你胆子够不够大了）

证明可微的时候，答案的放缩很精彩，对这个小结构应该要再敏感一点\(\frac{xy}{x^2+y^2}\leqslant \frac{xy}{2xy}=\frac{1}{2}\)

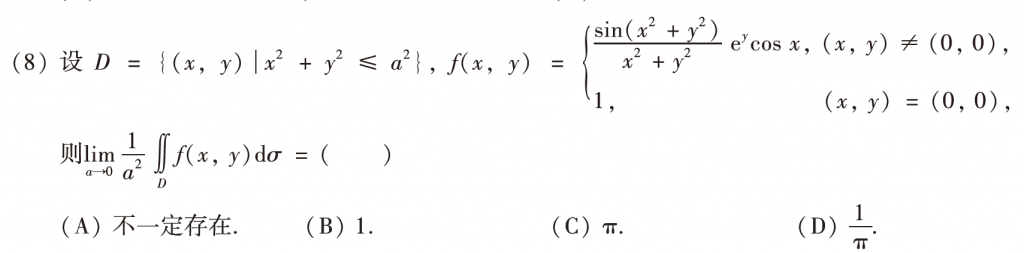
第八题感觉也一般般吧，二重积分中值定理直接秒了，高数讲义和880上都有类似的题。

第九题，应该是整套卷子最精彩的题了，一道题融合了很多知识点，我瞎做做对了，芳芳讲了这道题，非常清晰：点击这里

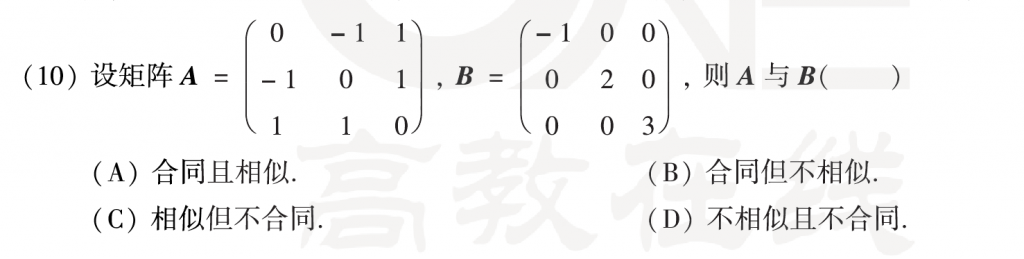
第十题也是基础题，直接通过迹可以推出俩矩阵不相似，然后再算一下A的特征值，发现和B有相同的正负惯性指数，实对称矩阵+相同正负惯性指数 -> 合同

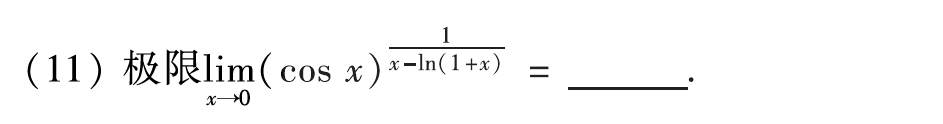
第十一题送分题，\(1^{\infty}\)型，用武老师讲过的三部曲直接秒杀

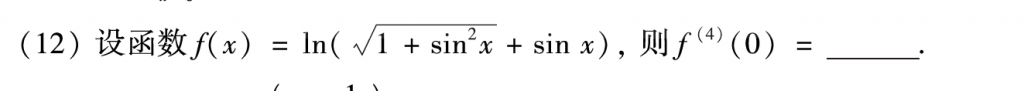
第十二题也简单，武老师强化课前几讲讲过类似的，求一次导奇偶性变化一次+奇函数在零点处为零。但是如果不知道这个结论的话，这道题应该几乎没法做。

第十三题我是用常规方法做的，算两个极限，武忠祥老师的简单方法我用的不熟没敢用，不然应该也可以直接秒杀，明天再复习下这块。

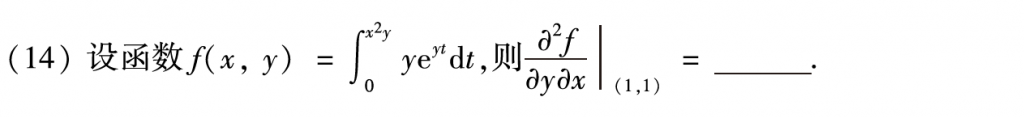
第十四题要注意对y求的时候，要先换元，因为积分里面，如果积分变量和求导的变量混着就不能用求导公式，有个加速的点就是先带后求。答案里还提到了一个先对x求导的方法，我确实没想到，因为感觉换元挺简单的，就没往下进一步想了。

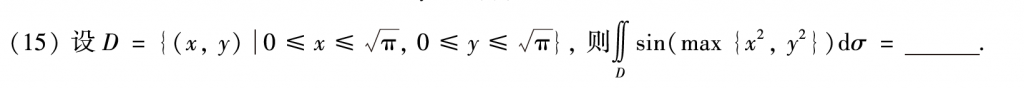
第十五题我感觉还是一道挺不错的题，把积分区域画出来后发现关于y=x对称，再加上被积函数里面有孤立的x方和y方，那么就肯定要想对称性了，这里的用的对称我感觉不是轮换对称，就是普通的对称，把x和y对调，然后积分区域也对调，那么两个二重积分其实是一样的，这个武老师强化课重点讲过的，印象还比较深。(高数讲义P180例题14可以好好做做，这道题搞懂了最这种题就没什么问题了)

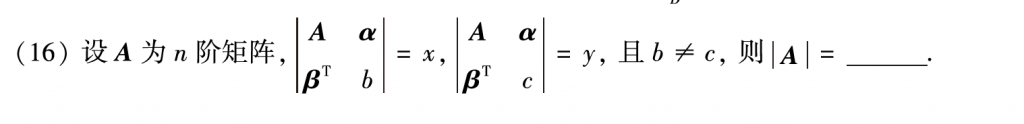
第十六题也是一道非常nice的题，这道题我当时没做出来，主要是确实没想到可以用行列式的拆分性质，复盘的时候我还想到了两个其他的解法。第一个就是直接把行列式里面的元素当成一个一个数给他乘开，然后两个式子相减就可以得到答案。第二个是使用初等变换，第一行左乘\(-\beta ^TA^{-1}\)加到第二行，把\(\beta\)那个地方的元素消成零，然后按照最后一行最后一列展开，就可以得到\(\left| A \right|\left( \beta ^T\times \left( -A^{-1} \right) \times \alpha +b \right) =x\)，对后一个行列式作同样的处理，两个式子相减，也可以得到最后的结果。

但是这两个方法虽然能解出来最后的答案，但是感觉第一个方法比较危险，没有科学依据，为此我还专门去查了分块矩阵的乘法：https://zhuanlan.zhihu.com/p/26285415，基本都要求几个矩阵是同型的。

第十七题也还可以，但是有个bug，左边的函数是周期为5的函数，右边的函数真的可以以5为周期吗？anyway，算切线主要就是要求\(f\left( 5 \right)\)和\(f'\left( 5 \right)\)，但是有个周期5的性质，那么就是算\(f\left( 0 \right)\)和\(f'\left( 0 \right)\)，\(f\left( 0 \right)\)的话两遍取极限就好了，算\(f'\left( 0 \right)\)我走了弯路，答案直接把3分成了两个\(f\left( 0 \right)\)，这样的话就很快了。我首先是把-x带到式子里面去，然后与原式子相减左边就变成\(f\left( x \right) -f\left( -x \right)\)，然后再用导数定义，这样的话比较慢，右边还得算两个极限。还有个易错点就是最后切线\(f\left( x \right) =f'\left( 0 \right) \left( x-5 \right) +f\left( 0 \right)\)，千万不能把\(\left( x-5 \right)\)写成\(\left( x-0 \right)\)，这个错误我以前犯过。

第十八题其实是很常规的题，真题里面无数次考过，求出来旋转体体积或者其他的东西，比如表面积等等，带参数，求最大最小就是求导。这道题我也慢了，我用二重积分在x>0的部分分区间算的，然后先y后x，这样我以为会简单点，但是计算量也蛮大的，我算错了...有个地方把y凑微分凑成y方的时候，前面少乘了个1/2，傻了。答案直接用公式算，然后被积函数是\(\left( a-y \right) ^2\)，这样的话也不用分区间讨论了，更快，又学到一手hh。

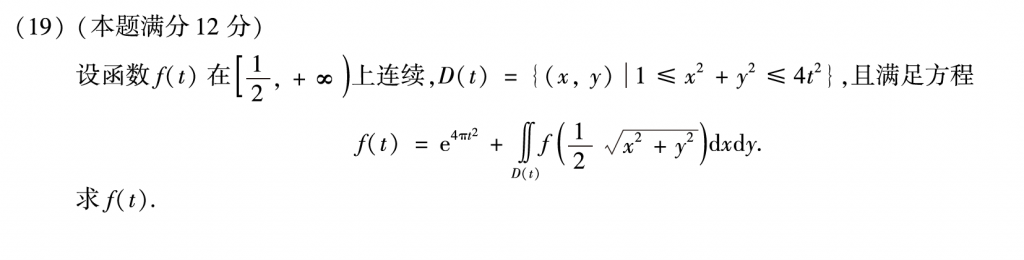
第十九题整道题做错了，着实不应该，12分直接没了，这道题我做过五六遍了，甚至答案都记得，但是我看掉了前面有个\(1\le x^2+y^2\)导致整道题做错，一般像这种题有两种方法，一种是把后面的二重积分设为一个常数，然后两边二重积分，对应高等数学辅导讲义P183的例题2。第二种方法就是把积分方程化成微分方程，就是这道题的解法。

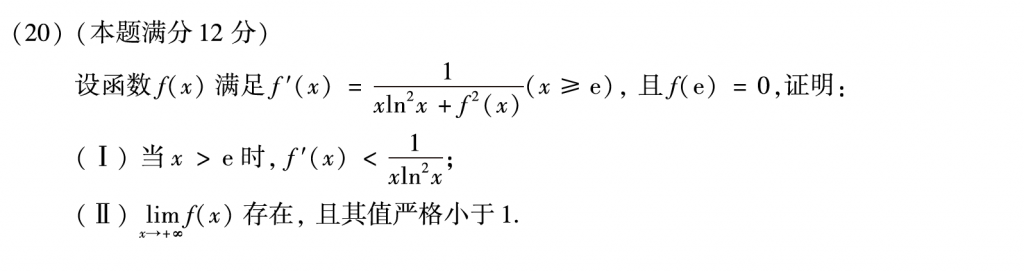
第二十题感觉也没啥意思，第一问\(f^2\left( x \right)\)肯定大于等于零，然后x>e推出f不等于0，直接放缩就严格小于了。

第二问也简单，根据第一问的结论先放缩一步，左边右边都有一种积分的欲望，那么就两边积分就好了，然后单调有界，其他的就没啥了。

第21题也很朴素，第一问肯定没问题，套公式、二重积分都可以。第二问我没做出来，关键在于我不知道页面上升的速率应该怎么表示，看了答案才知道是\(\frac{dh}{dt}\)，可惜，本来是一道很简单的题，物理应用这块还真应该花一天的时间再好好突破一下：点击这里，这是我收藏的课，还没听。

第二十二题也很常规，把B按列分块，然后在B里面随便找两个无关的向量就可以作为A中特征值为-2的特征向量。然后第二个条件两边直接转置，就可以得到C的一列作为特征值为2的特征向量，然后可以相似对角化，计算三个矩阵相乘A就出来了。我觉得比较麻烦的就是求逆矩阵和三个矩阵相乘，我老是算错，做的时候可以用一下检验方法，比如求完逆之后可以和原矩阵乘一下，看是否为单位阵。昨天晚上bilibili给我推了个视频，有个方法我感觉特别好：点击这里，之后可以用用。

第二问也简单，没什么好说的。

第一套总结

感觉小题确实有东西，你说不难吧，其实做起来还是有点费劲的，说难吧，考的又都是很基础的东西，尤其是线代，我觉得三道小题都很棒，可以学到东西。整套卷子的大题稍微弱了点，但是我大题做的不好，第18题积分计算失误，第19题题目看错，第21题物理应用条件转化不会，这些都是这个阶段要重点努力的点。

第二套

今天是2021-11-06，上午花了三个小时做了李艳芳的第二套模拟卷，把我的心态做的有点崩，选择题还好，只错了一个，填空题错了三个，大题基本一半不会，直接把我干碎了，三个小时做满，最后出分87......目前做模拟卷的最低分，希望到最后也是最低分，不然小心脏真扛不住。

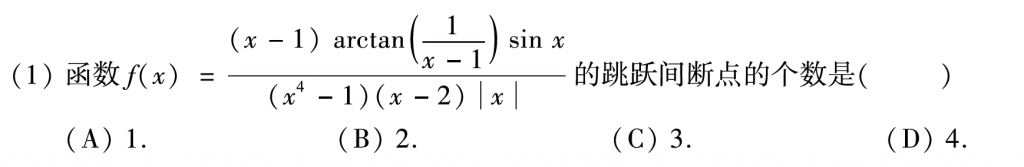
第一题感觉还是比较常规的，1，-1，0，2一个一个观察就好了

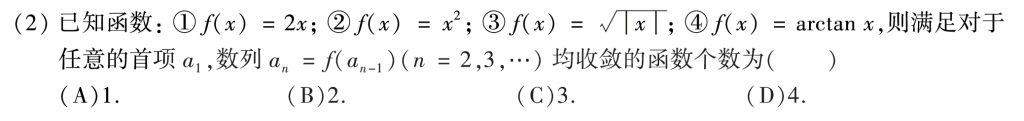
第二题的话，前两个很好排除，直接令a1 = 2，然后发现越迭代越大，那么肯定就是发散的，第三个其实我做的时候也是带值进去算的，每次都会在前一个数的基础上多一个根号，虽然选对了但是感觉其实不是很严谨，复盘的时候看了下答案感觉还是有点复杂，太严谨了，考试的时候没必要用这种方法，可以用递推数列的压缩映像：\(|a_{n+1}-a_n|=|f\left( a_n \right) -f\left( a_{n-1} \right) |=f'\left( \xi \right) |\left( a_n-a_{n-1} \right) |\)，三和四都满足\(|f'\left( \xi \right) |<1\)，所以会收敛（这块我了解的不多，有懂的大佬可以在评论区说下这个做法对不对）

第三题不难，按照分段可以把y给求出来，但是这道题我一开始选的A，因为感觉不能确定y是否连续，而第二段有一个任意常数，但是做了后面几道题之后发现微分方程里面y'都出来了，y肯定连续，然后可以把C确定下来，然后就选B了

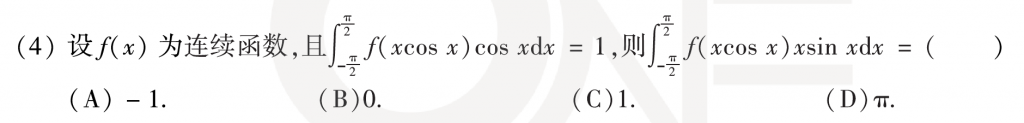
第四题很难，拿到这道题的第一想法是奇偶性，但是搞了一会没搞出来，然后发现两个式子肯定有关系，想到武老师讲过的排除法，把任意函数f(x)定下来，我是直接把f(xcosx)当成一个常数，把第二个式子里面的sin凑进去之后用分部积分，然后神奇的发现和第一个式子一样，然后就选了C。答案的方法一挺巧妙的，两个式子相减之后可以直接凑微分，但是我感觉大部分人应该想不到......方法二也是用的排除法，但是他的后续操作我感觉也有点麻烦，没我这个快。

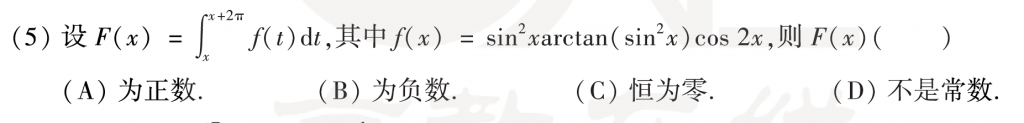
第五题也很麻烦，对这个F(x)拿到后的第一件事就是求导，求完导之后发现直接就是零了，那么肯定就是常数了，然后只需要随便带一个值进去，算出\(f\left( x_0 \right)\)就可以得到结果，现在的问题就在于x的取值以及后续如何计算，我一开始直接令x为0，发现这个积分几乎处理不了，然后就想到了\(-\pi\)，对称区间肯定就要想有无奇偶性，发现里面是偶函数，可以缩小一半区间，然后接下来的操作我想了蛮长时间的，感觉有点无从下手，问题就在于那个arctan上，想了一下发现它有界，然后就直接放缩了\(\int_0^{\pi}{\sin ^2t\text{arc}\tan \left( \sin ^2t \right) \cos 2tdt<}\frac{\pi}{2}\int_0^{\pi}{\sin ^2\cos 2tdt}\)，然后把cos2t凑进去之后分部积分再计算就出来了。答案的方法...胆子真的大，那么大个块头，我是不敢直接分部积分的。

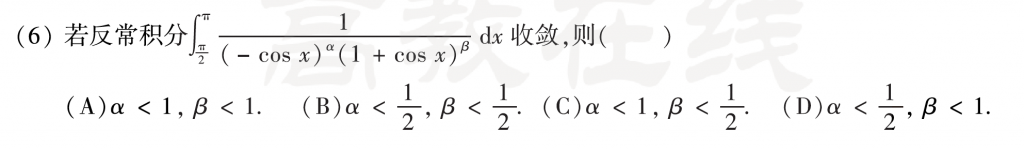
第六题感觉还是比较常规的吧，首先找瑕点，发现是\(\frac{\pi}{2}\text{、}\pi\)，那么分区间，前面一个区间在算的时候不用管1+cosx，后面区间算的时候也是一样，不用管前面的，然后分别取极限比阶就好了，如果有读者对这块不太熟练可以做做张宇1000题上面的，具体页面我明天看下，把上面的几道题做会这种题就没什么问题了。

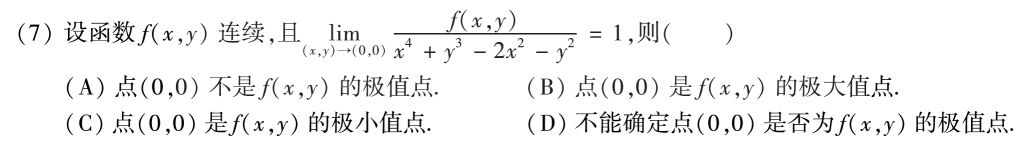
第七题虽然我的方法做对了，但是不能确定是不是经典的错误，说一下我的方法，分母里面\(x^4\)是比\(x^2\)高阶的无穷小，直接划掉，然后\(y^3\)是比\(y^2\)要高阶的无穷小，也可以直接划掉，分母提取负号之后恒大于零，根据连续+保号性，就能推出最后的结果了。（这个地方有可能有问题，因为是二元函数，我不清楚是否有这个性质！）

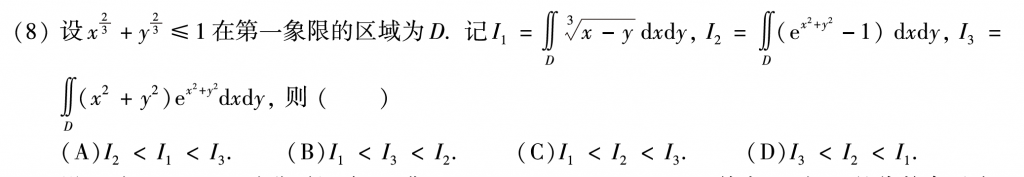
第八题我觉得也是很有难度的一道题，看到那个D的方程我就知道是星形线了，但是感觉后面的三个积分比大小和这个星形线没有关系，事实也确实如此，有用的就只有第一象限。第一个积分我看了一会没什么思路，然后第二个积分我首先想到的就是放缩\(e^{x^2+y^2}-1\ge x^2+y^2\)，然后再根据第一象限可以发现是恒大于0的，然后这时候再去看第一个积分，发现在第一象限有正有负，而后两个积分都是大于零的，所以现在就只用看后两个积分谁大谁小了，比较被积函数的大小即可，主要的方法就是化成一元。

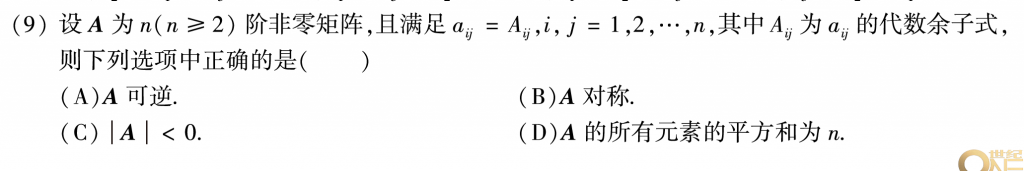
第九题是我唯一错的一道选择题，说实话很不应该，因为我的笔记本总结的第一个类型的题就是这个，还特意标了非零矩阵可以推出行列式大于零或者小于零，但是时间一长就给忘了，菜是原罪。

第十题是非常简单的的一道题，根据题目给的条件+迹可以知道特征值为1、1、2、2，然后根据行列式等于特征值之积可以把a给定下来，然后就看两个二重特征值各自是否可以提供两个线性无关的特征向量即可判断A是否可以相似对角化。

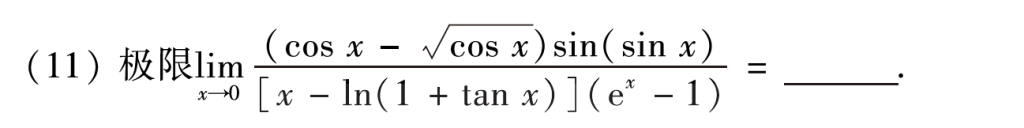
第十一题是送分题，不过这道题也有加速的点，比如对分子的处理\(\cos x-\sqrt{\cos x}=\cos x-1+1-\sqrt{\cos x}=-\frac{1}{2}x^2+\frac{\frac{1}{2}}{2}x^2=-\frac{1}{4}x^2\left( x\rightarrow 0 \right)\)，这里给大家补充一个公式，武老师在基础班就讲过的，因为很细节所以很多人可能不知道：\(1-\cos ^lx=\frac{l}{2}x^2\)，这个公式很好推。分母处理也简单，\(x-\ln \left( 1+\tan x \right) =x-\tan x+\tan x-\ln \left( 1+\tan x \right) =\tan x-\ln \left( 1+\tan x \right) \left( x\rightarrow 0 \right)\)，因为x-tanx是三次，后面是二次，直接扔掉不管。吐槽一句，答案编的是个什么玩意，考场上如果按照答案的方法做绝对慢了一个次量级。

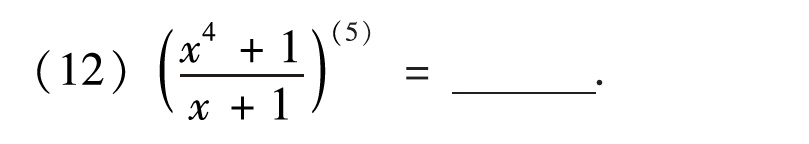
第十二题我第一眼感觉非常棘手，甚至有一种不祥的预感，但是化简后发现就这...\(\left( \frac{x^4+1}{x+1} \right) ^{\left( 5 \right)}=\left( \frac{x^4}{x+1}+\frac{1}{x+1} \right) ^{\left( 5 \right)}=\left( \frac{x^4-1+1}{x+1}+\frac{1}{x+1} \right) ^{\left( 5 \right)}=\left( \frac{\left( x^2+1 \right) \left( x-1 \right) \left( x+1 \right)}{x+1}+\frac{2}{x+1} \right) ^{\left( 5 \right)}=\left( \left( x^2+1 \right) \left( x-1 \right) +\frac{2}{x+1} \right) ^{\left( 5 \right)}\)

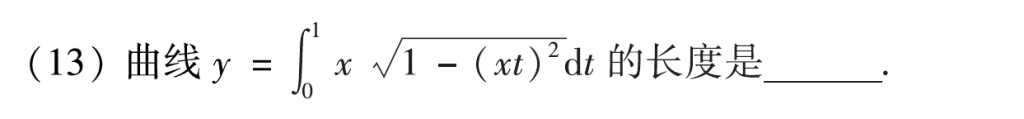
第十三题我做错了，x的范围我搞成0到1了，正解是-1到1，这种题我在1000题上做过类似的，主要是根据根号的定义域和t的取值范围可以确定x的范围，我这里确实存在思维缺陷，没想过x小于0的情况，以后得好好注意下了。

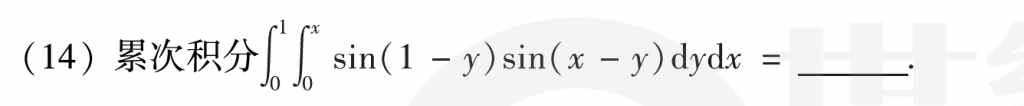
第十四题我也做错了，像这种裸的二重积分99%都是交换次序，思路上没什么问题，但是我犯了很低级很低级的错误：

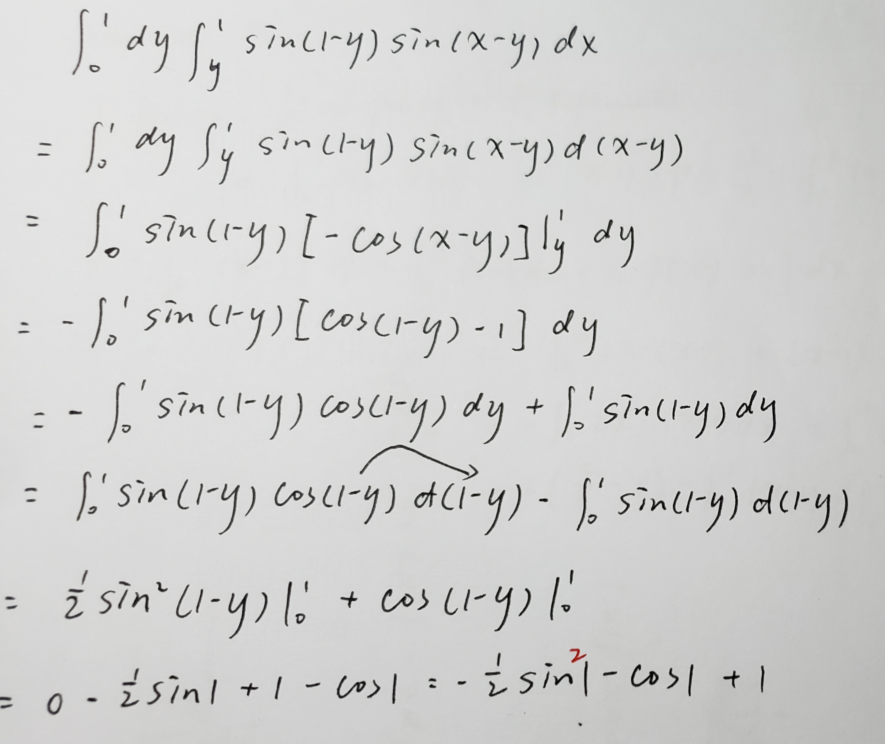
复盘的时候，一步一步算，最后还是把这个平方给漏了......细心这块没赢过。

第十六题我也做错了，我的方法是找不同行不同列...也就是最原始的计算行列式的方法，然后就不知道为啥找错了，也懒得复盘了。答案的方法太高科技了，我从来没想过还能这么操作的，题目要求常数项，可以直接把x=0带进去，然后算行列式就ok了，真厉害，又学到一手。

第十七题应该没人不会做吧，偏积分就好了，全微分我用的属实不习惯，第二问也简单，没什么好说的。

第十八题这题我整道做错了，我以为\(u'=\frac{du}{dx}\)，然后y和z是x的函数，设xyz=r，那么\(u'=\frac{dr}{dx}\cdot \left( yz+x\frac{dy}{dx}z+xy\frac{dz}{dx} \right)\)，然后还倒了半天，没搞出来，主要是之前这过这种题，被影响了，不知道大家还记不记得\(z=u\left( r \right) \text{、}r=\sqrt{x^2+y^2}\)，大概是这种，因为这种题我做过好多好多次，所以以为这道题也是这种，实际上yz不一定是x的函数，他们三者应该是独立的。

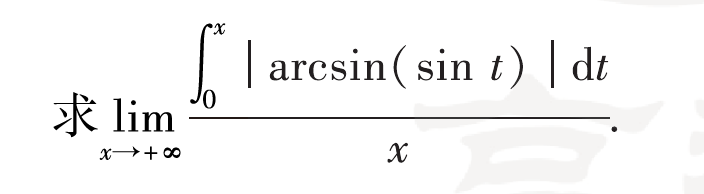
第十九题是真没辙，我想了好长时间，没想出来，我感觉能把这道题做出来的应该没几个人，除非你对真题研究的非常透彻，因为这道题是2000的数学二的一道题改编的：

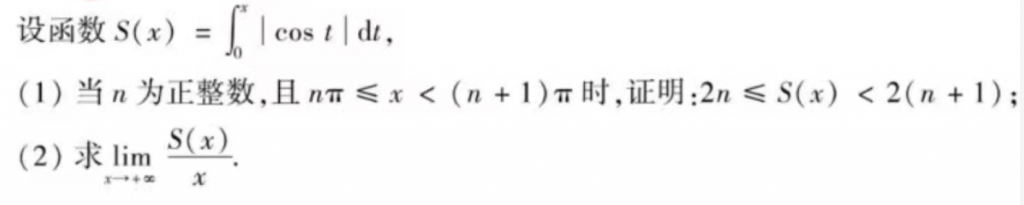
说来惭愧，这道真题我做了大概三四遍了吧，第一遍是汤家凤强化课的定积分不等式部分，第二遍第三遍应该分别是在严选题和880，然后前一两个月真题也做到了，但是这道模拟题由于把第一问去掉了，还是没辙。总结一下这种题的做法：第一步就是确定绝对值函数的周期，一般都是\(\pi\)，不过也不好说，得具体问题具体分析，然后第二步就是算一个周期内的积分，最后设x的范围是n个周期到n+1个周期，算出n个周期的时候S(x)的值以及n+1个周期的时候S(x)的值，最后用夹逼准则。（希望以后这种题能做出来，很有区分度的）

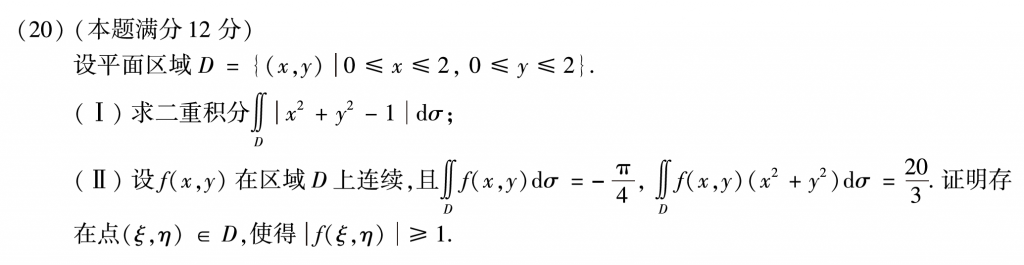
第二十题我觉得比较简单，第一问没问题，把区间分成D1和D2去绝对值，然后D2不好算可以用D减去D1，这种带绝对值的一般都是这种处理手法。第二问的话，一定要找到和第一问的联系，因为你会发现第二问给的两个数字，和你第一问算的东西一模一样，然后相减就完事了。外面套上绝对值，用绝对值不等式放缩一步，最后一步我没想到用闭区间有界性质，我自己脑补了一个二重积分的第一中值定理，然后做出来了，复盘的时候在百度上查了一下发现居然真有。

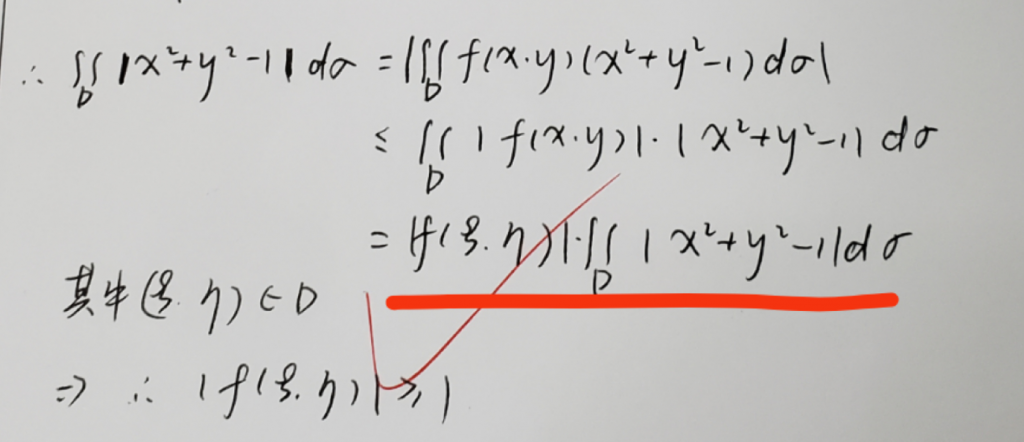
第二十一题也是基本下不了笔，我甚至都没想过用数列极限，这道题真的是难。我说一下我的思路，应该能给你一些启发，首先证明f(x)恒为常数，那么可以把这个问题转化成\(f'\left( x \right)=0\)，不管对不对，我觉得这个想法肯定是没问题的，然后题目只说在定义域上有定义，那肯定不能直接求导什么的，我想的是用导数的定义\(\underset{h\rightarrow 0}{\lim}\frac{f\left( x+h \right) -f\left( x \right)}{h}\)，而且题目正好给了两个函数相减，我就在想能不能凑一个导数定义出来，想了很长时间，没辙，遂放弃。其实题目那个条件f(x)=f(1-cosx)，我第一冲动是拉格朗日，但是条件不够，就算拉了也做不出来。这道题我看答案云里雾里，有懂的大佬可以加我个好友一起交流下（微信：mach4101, qq：2971746737）。

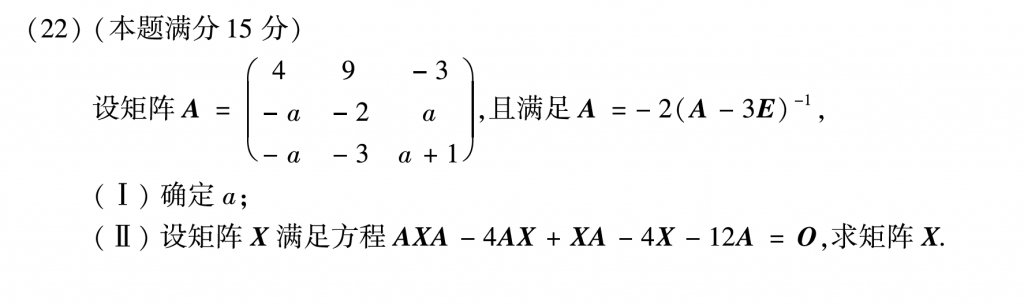
第二十二题质量非常高，这道题我只做了第一问，第二问想到的方法计算量爆炸，遂放弃，第一问应该还是比较简单的，答案的方法用特征值我觉得繁琐了，其实两问都没必要引入特征值。说一下我的思路：根据条件可以推出\(A\left( A-3E \right) =-2E\)：

$$
\left[ \begin{matrix}
4& 9& -3\\
-a& 2& a\\
-a& -3& a+1\\
\end{matrix} \right] \left[ \begin{matrix}
1& 9& -3\\
-a& -1& a\\
-a& -3& a-2\\
\end{matrix} \right] =-2E
$$

然后直接第一行乘第一列等于-2，就可以把a给算出来。

第二问技巧性非常强，我化简到\(\left( A+E \right) X\left( A-4E \right) =12A\)之后就开始走弯路了，我的想法是构造方程组求解，但是右边计算量是在太大了，而且最后也就几分钟，就没做了。

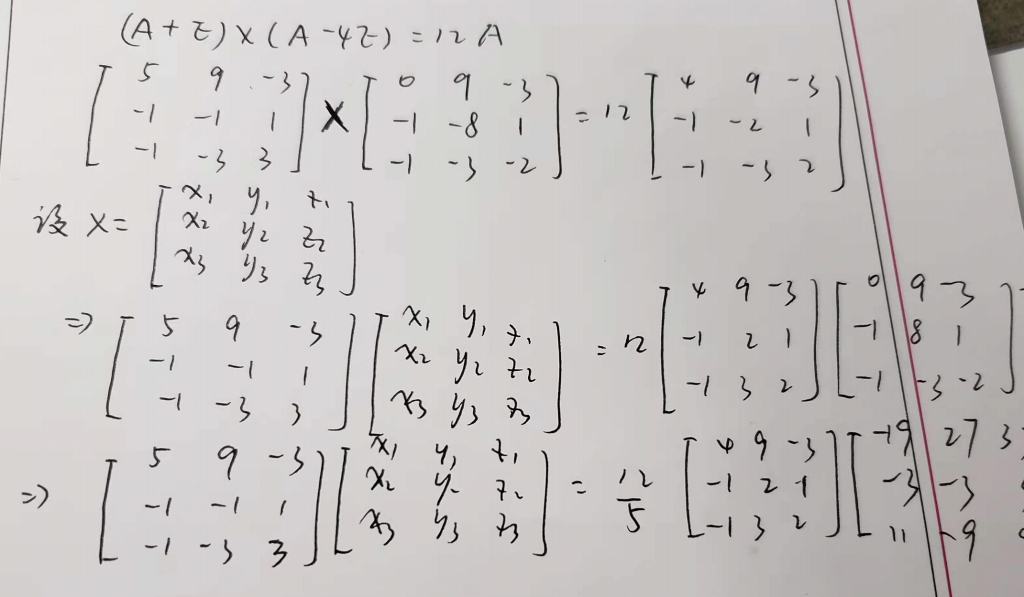
说一下答案的思路，首先把A左右两边的东西都除到右边（除不严谨，感性理解即可），前提当然是两个矩阵都要可逆，如果要判断两个矩阵是否可逆，有一个非常快捷的方法：如果两个矩阵相乘的结果是一个逆矩阵，那么这两个矩阵均为逆矩阵，如果碰巧结构是单位阵，那么这两个矩阵彼此互逆，这个用行列式可以推，答案用特征值属实没必要，相乘结果如下：

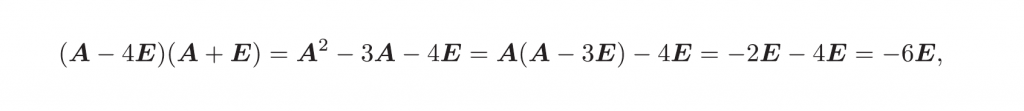
然后可以推出\(\left( A+E \right) ^{-1}\)和\(\left( A-4E \right) ^{-1}\)，然后带进去化简就能得到最后的结果：

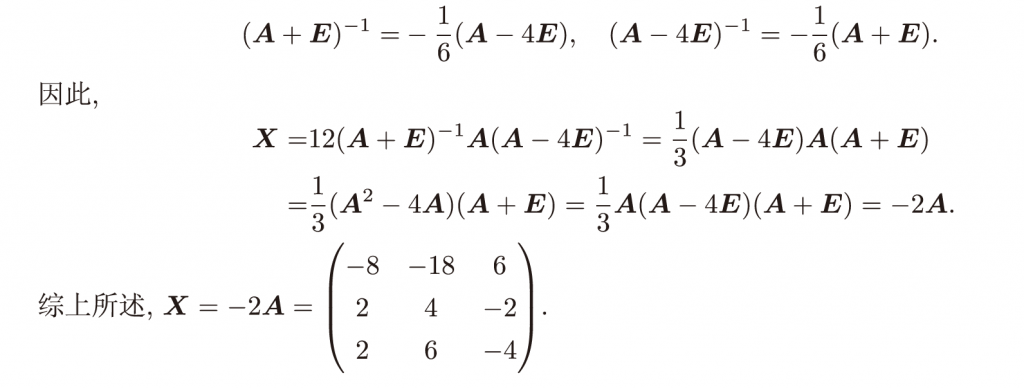
第二套总结

这套卷子我觉得质量是非常高（非常难），花了我两天时间，除了倒数第二题，基本算是吃透了，感觉提升真的很大。当然也有不好的点，比如很多答案都不是最优解，甚至没有我一个普通学生想的方法好，以芳芳的实力，肯定不止如此，可能写书还是应该追求严谨，（以免被武老师发现漏洞然后批判一番，我在武老师的发的一张照片上看到了芳芳的书hhh）。但是对于那些想通过解析来弄懂一道题的同学来说不是那么友好。

小题没有一道送分题，反常规、反思维定势，就算是简单的题，也会有坑，大题更不用说了，第二个大题是由于我的思维定势导致想复杂没做出来，第三个大题考察对真题的挖掘程度，第四个大题第一问绝对值积分，比较常规，但是也有技巧，第二问需要刻意联系第一问，然后结合多元函数的有界闭区域最值定理，或者我所拓展的二重积分的第一中值定理，真的精彩。第四个大题拿到直接罚坐，是一道极具区分度的题，我敢打包票这道题如果你能在考场上独立做出来，清北华五冲就完事了。最后一道线代大题也极具区分度，非常的偶数年，不会技巧就爆炸计算量，会技巧就能节省大量时间，但是我还是不懂为什么要引入特征值，感觉没什么必要。

第三套

今天是2021-11-08，上午花了三个小时做了芳芳的第三套试卷，其中选择题错一道、填空题错一道、大题错三道，出分107，感觉这一套选填难度比上一套要小很多，大概6，70分钟就做完了，但是后三道大题做的太差了。

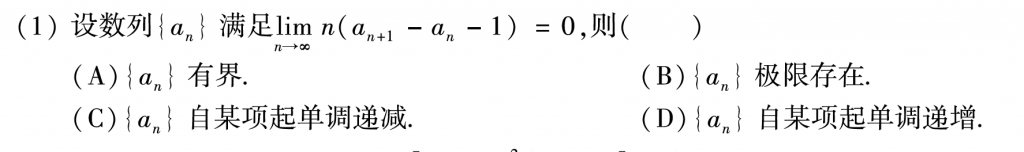
第一题我就感觉是比较有难度的，首先极限存在的话，前面是无穷，后面那项肯定是0，也就是说\(\underset{n\rightarrow \infty}{\lim}\left( a_n-a_{n-1}-1 \right) =0\Longrightarrow \underset{n\rightarrow \infty}{\lim}\left( a_n-a_{n-1} \right) =1\)，那么就可以推出单调，但是有界我推不出来，所以就选了D，答案直接举例，可以积累一波。

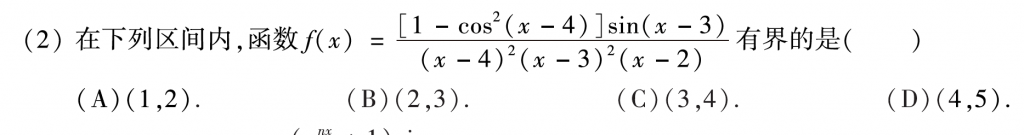
第二题是真题改编的，这种类型的题我在1000题和真题集里面都做到过，主要就是如果\(f\left( x \right)\)在开区间上连续，如果要证明有界的话，只需要证明极限趋向端点的时候存在即可，算是闭区间上连续的函数一定有界的推广。

第三题我称这种函数为动态函数，主要就是分区间讨论就好了\(e^{nx}\)还是比较好搞的，那个\(x^n\)比较麻烦，武老师的讲义上总结的有，忘了可以再看看。

第四题也很基础，可以直接把极限拆开，因为前面\(\frac{\sin x-x}{x^3}\)，极限存在，整个极限存在，后一项一定是存在的，然后可以用一次洛必达+导数定义就出来了，不能两次洛必达，二阶导不一定连续，条件不够。

第五题就是送分题，求个导就好了，估计难的点就在于把积分里面的x方提出去再求导，这个也是很基础的东西。

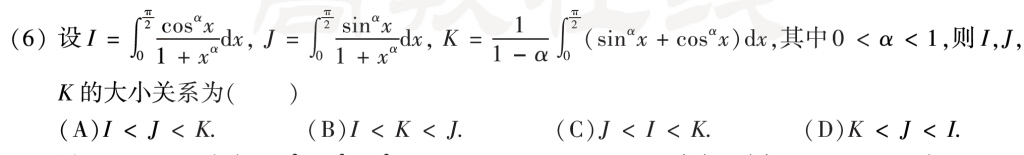
第六题挺有意思的，我又是用几何的方法做，然后做对。答案我看了一眼就没看下去的欲望了，考场上用这种计算的方法不是很好。说一下我的方法，非常不科学，但是能搞出来，我先看I和J，发现一头雾水，然后看K，发现和I、J有联系，所谓相似找差异，差异就在于分母的不同，很显然，前两个的分母是大于1的，而K的分母小于1那么就会更大，甚至比前两个加起来还要大，所以排除BD，再AC里面找，就只需要确定I和J的大小关系，之后的思路就很玄学了，cos那一项在\(\left[ 0, \frac{\pi}{4} \right]\)上是要大的，而这个时候，分母还挺小，而在\(\left[ \frac{\pi}{4}, \frac{\pi}{2} \right]\)上，虽然sin大，但此时分母就大了，所以我推测I是要比J大的，所以选了C，五分到手，非常不严谨的思路，大家看看就好。

第七题没啥好说的，比谁算的又快又准而已

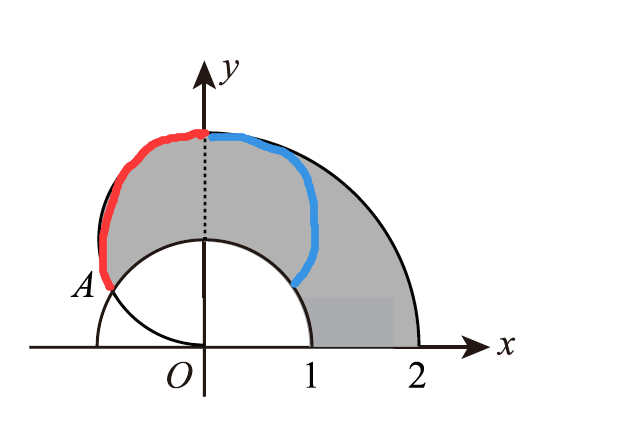
第八题也不难，确定积分区域之后发现如果先r后theta的话，肯定得分区间，AB排除，先theta后r，这个时候主要是确定theta的上限，显然是D选项，如果是到我画蓝色线条的部分，那就是C。关于这个先theta后r的题，武老师强化课讲过一道很经典的题，把那道题搞懂就没什么问题了，明天我给大家拓展一道880上的题。

第九题也很简单，①很好确定，如果你学过线性空间的话，可以秒选，三个无关的三维向量可以撑起一个三维空间，三维向量处于三维空间中，那么一定可以由这三个向量线性表示。②也好排除，如果\(\alpha _4\)可以由其他的向量线性表示的话，可能都在同一条直线上，那么秩为1。③太绝对了，反例可以随便举。④也简单，既然有向量不能被这个向量组表示，那么这三个向量撑起的空间肯定坍塌了，有可能是二维也有可能是一维。

第十题我做错了，这道题做错只能说明自己不懂得变通，行满秩，然后左乘一个P等于0，把P行分块，和列满秩然后右乘一个P等于零，把P列分块，实际上是一样的，方程组只有零解，那么P肯定为0。B的话直接前提是要列满秩。我错选的是C，确实是傻逼了，举一个比答案简单的反例：

$$
\left( \begin{matrix}
1& 1& 0\\
\end{matrix} \right)
$$

这个时候你动都动不了，更不用说化成题目的那种形式了。

D选项简单，行满秩了，那么矩阵和增广的行秩肯定相等，那么方程组有解。

第十一题，第一眼还是感觉有点抽象的，仔细分析之后发现就是常规的放缩＋定积分定义，然后有一步比较关键的是换分母手法：

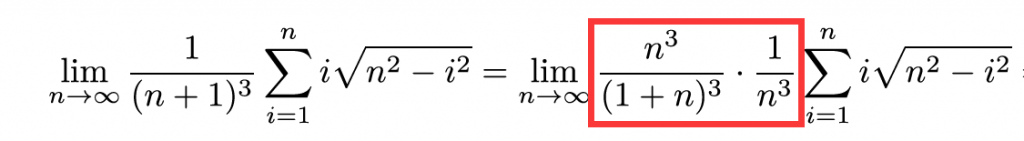
这个手法真的好用，可以在这里用，导数定义那块也能用上，多元函数微分里面也能用到。

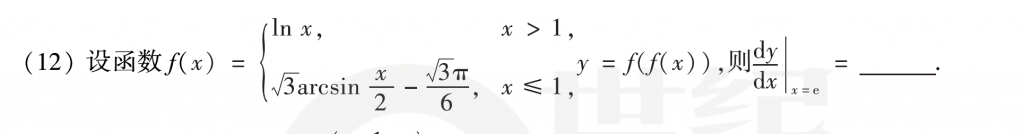
第十二题比较简单，没什么难度，无非就是复合函数求导+导数定义求导，我算\(f'\left( 1 \right)\)用的是导数定义，答案里面那个注可以学习一下，以后再遇到就能加速了，虽然感觉好像也一般？

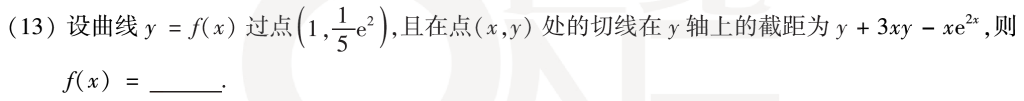
第十三题简单，这种题我都快做吐了，微分方程+几何

第十四题，对sinx进行挖掘，可以推出\(\alpha =0, \beta =1\)，然后对xe^x进行挖掘，可以推出x=1是微分方程的二重根，然后构造通解就好了。

第十五题我做错了，我是真没想到力还是有方向的，更没想到x轴方向的还能抵消，开眼界了，真题里面做到过一道类似的，明天晚上传上来给大家看看题源，比这个简单多了。

第十六题，也很简单，零特征值可以推出Au=0，那么其次的通解就是\(y=cu\)，然后非齐次凑一下就好了。

第十七题比较简单，这种带绝对值的肯定就是要分区间，化简后求个导找单调区间，求极值用零点定理就好了，有一步我觉得还是比较难的：

这一步放缩真的是神来之笔，我想了半天怎么搞这个积分，没辙，然后直接说大于0的，有猜的嫌疑...hhh

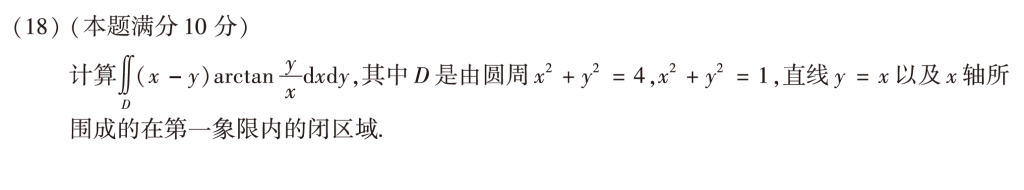
第十八题感觉有送分的嫌疑，两三分钟就做完了，甚至一度怀疑自己是不是做错了，果然这时候我还太年轻，不知道18题馈赠的礼物，早已在后三道答题中标好了价格......

第十九题做过两遍，这是第三遍，第一遍是武老师的严选题，第二次是在真题。没什么难度，就是利用曲率来构造方程，然后解微分方程就好了，唯一的难点在于倾角的使用：\(y'\left( x \right) =\tan \alpha\)，这道题没做出来多半是这个地方的问题，因为我第一次做也不会...

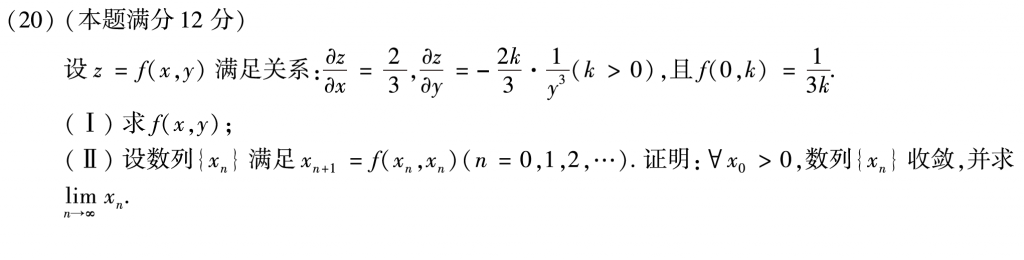
第二十题第一问肯定没什么问题，直接偏积分就好了，已经是第二次出现在三套卷里面了。第二问我没做出来，我的思路其实是和答案一样的，就是先证明\(x_n\)有界，然后用这个有界的条件去证明单调，但是我有界证明的那一步积分没想出来，很可惜：

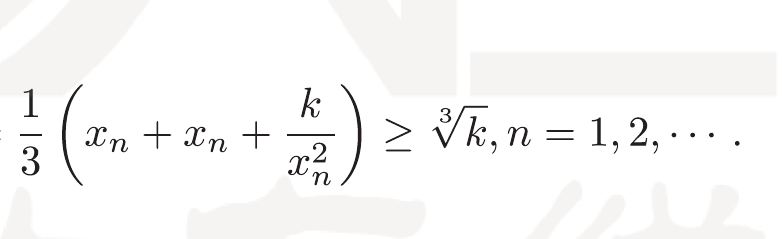
主要就是这个公式没注意到：\(a+b+c\geqslant \frac{\sqrt[3]{a+b+c}}{3}\)，均值不等式那一块还得多看看，感觉这就是所谓的基础，确实基础不牢地动山摇。

第二十一题我第一问就做错了，求完导数把零带进去之后肯定就是算\(f_2\left( 1,0 \right)\)，受到\(f_1\)的影响，我以为\(f_2\left( x,1-x \right) =-x\)，然后就算错了......果然还是应该老老实实把原来的式子拿来对x求导，然后算\(\(f_1\)\)

第二问我没什么想法，我是真没想到还能利用参数方程把前面的单位圆和后面的方程联系起来...长见识了，然后\(\frac{\partial f}{\partial u}=f_{1}^{'}\left( \cos t,\sin t \right)\)，这一步等式虽然简单，但是感觉也很难想到。后面的也很难想...感觉这道题纯粹是给我这样的菜鸡开眼界用的...

第二十二题我也没做出来，是一道非常棒的题，首先看到二次型都是平方其实就要想正定了，这个思路我在张宇的线代9讲、杨超必做习题库和真题里面都见过：

果然是好久没做无关的证明题了，推出正定之后我就不知道后面应该怎么做了，设k1,k2,k2都没想到......后面就要利用已知条件，乘一个东西，然后推k1，k2，k3全为零，真的是很棒的一道题，可惜没做出来...

第三套总结

这一套的选择填空我感觉还是一般般的，不过这个一般般是相较于前面的两套试卷来说，总体水平很强。大题19题考了个倾斜角，没见过应该挺麻烦的，第20题的那个放缩，印象真的深，第21题第二问的一系列手法，把我看懵了，第22题结合正定和向量无关的证明，在加上判断正定时用到的方程组，还是很综合的。