本讲主要描述浮点数和整数如何在机器内编码和存储(大端和小端),了解这些细节后,能够更好地理解代码中进行数值计算和比较时出现违反直觉的结果,同时也能避免出现这样的问题。
信息的二进制编码
在机器中,所有的数据主要分为两类:
- 数值数据:包括无符号整数、带符号整数、浮点数
- 非数值数据:逻辑数(包含位串)、西文字符和汉字
而在机器内部,无论是数值数据还是非数值数据,都是用二进制来编码的,这部分的原因我就不详述了,主要是因为二进制在机器内部非常容易实现,与之而来的还有两个概念:真值和机器数
- 真值:真正的值,也就是现实生活中带正负号的数
- 机器数:用0和1编码的计算机内部的0/1序列
定点数的编码表示
先来介绍一下各种码:原码、补码和移码,反码用的很少,了解一下就可以了。
原码
先观察一下下面的这个表格:
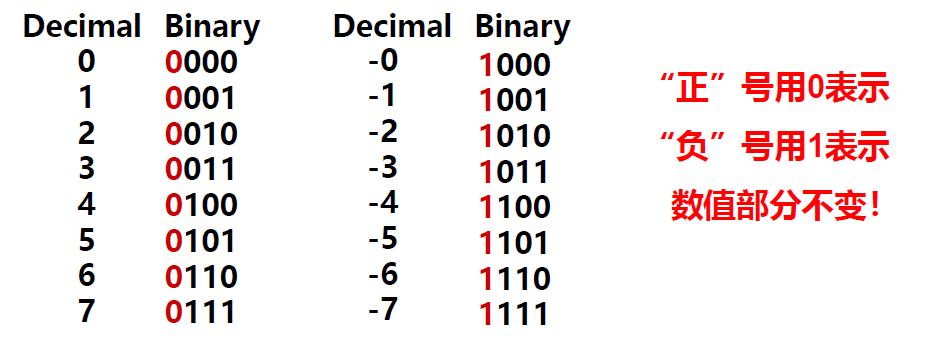
可以看出,只是将十进制数的绝对值转换成二进制数,然后最高位作为符号位就好了,最高位为0就是正数,最高位为1就是负数。
这种编码非常容易理解,但有一系列的问题:
- 0的表示不唯一,不利于程序员编程
- 加减运算方式不统一
- 需要额外对符号位进行处理,不利于硬件设计
- 当a<b时,实现a-b比较困难
从50年代开始,整数都用补码来表示,但浮点数的尾数用原码定点小数表示
补码
补码的定义其实就是一个同余方程,学过数论的同学应该对这玩意非常熟悉,现在我来简单的介绍一下
在一个模运算系统中,一个数与除以“模”后的余数等价。
比如时钟就是一种模12系统,假定钟表指针指向10点,现在要将他拨到6点,有两种方法,一种是倒拨4格:10-4=6,另一种是顺拨8格:10+8=18 % 12=6,所以,在模12系统中:10-4 = 10+8(mod 12),-4 = 8 (mod 12),则称8是-4对模12的补码。
结论:
- 一个负数的补码等于模减去该负数的绝对值
- 对于某一确定的模而言,某数减去小于模的另一个数,总可以用该数加上另一个数负数的补码来实现,也就是可以用加法实现减法
举个栗子:假定时钟只能顺拨,从10点倒拨4格后是几点?
$$
10-4=10+\left( 12-4 \right) =10+8=6\left( mod12 \right)
$$
栗子2:假定算盘只有四档,且只能做加法,则在算盘上计算9828-1928等于多少?
$$
9828-1928=9828+\left( 10^4-1928 \right)
\\
=9828+8072=17900=7900\left( mod10^4 \right)
$$
由于运算器的运算位数有限,假设为\(n\)位,则运算结果只能保留低\(n\)位,故可以看成是个只有\(n\)档的二进制算盘,因此,其模为\(2^n\),所以根据补码的定义,假设补码有\(n\)位,则:
$$
\left[ X \right] _{\text{补}}=2^n+X\left( -2^{n-1}\leqslant X<2^{n-1}, mod2^n \right)
$$
其中,\(X\)是真值,\(\left[ X \right] _{\text{补}}\)是机器数
求真值的补码
假设机器数有8位,求123和-123的补码表示:
如何快速得到123的二进制表示?
123=127-4=01111111-100=01111011,所以-123=-01111011
所以补码:
$$
\left[ 01111011 \right] _{\text{补}}=2^8+01111011=01111011\left( mod2^8 \right)
$$
$$
\left[ -01111011 \right] _{\text{补}}=2^8-01111011=100000000-01111011=11111111-0111011+1=10000101
$$
总结:正数的补码等于其真值,负数的补码为其真值各位取反,末尾加一,简称为取反加一,取反加一也有一种快速方法:从右往左第一位1开始,右边的不变,左边的全部取反:

求补码的真值
直接说结论:
- 符号为零,则为正数,数值部分相同
- 符号位1,则为负数,数值各位全部取反,末位加一(也可以用我上面说的简单方法)
移码
移码也很简单,就是将每一个数值加上一个偏移量(Excess/bias)
通常,当编码位数为\(n\)时,bias取\(2^{n-1}\)或\(2^{n-1}-1\)(如IEEE 754标准)
举个栗子:\(n=4:E_{biased}=E+2^3\left( bias=2^3 \right)\)
$$
-8\left( +8 \right) ~0000
\\
-7\left( +8 \right) ~0001
\\
\cdots
\\
0\left( +8 \right) ~1000
\\
\cdots
\\
+7\left( +8 \right) ~1111
\\
$$
观察发现,其实就是将所有数字都映射到\(0~E_{biased}\)上,所以说,我们一般用移码来表示指数(阶码),后面会具体讲到,就是为了方便比较大小。

整数的表示
整数主要分为带符号(signed)和无符号(unsigned),需要注意的是无论是带符号还是不带符号,整数在内存中都是通过补码来表示的,正数和0的补码就是该数字本身,负数的补码为其对应的正数取反加一。
无符号数
一般在全是正数运算且不出现负值结果的场合下,可以使用无符号数,如地址运算之类的,其与带符号数相比,最大的不同就是没有符号位,也就是因为没有符号位,所以他可以表示的数的最大值比带符号的要大,所以在C语言中,一个数大到练unsigned long long也存不下的话,就得开始考虑高精度模拟了。
带符号整数
从上个世纪50年代开始,所有的计算机抛弃原码,使用补码来表示带符号整数,其主要原因如下:
- 补码运算系统是一种模运算系统,加、减运算统一,也就是说,可以使用加法来实现减法
- 0的表示唯一,方便使用
- 比原码多表示一个最小负数
另外,如果在运算中,同时出现无符号和带符号整数,C编译器将带符号整数强制转换成无符号数,比如说对于如下关系表达式,某些结果并不符合直觉,就是由于这个原因:
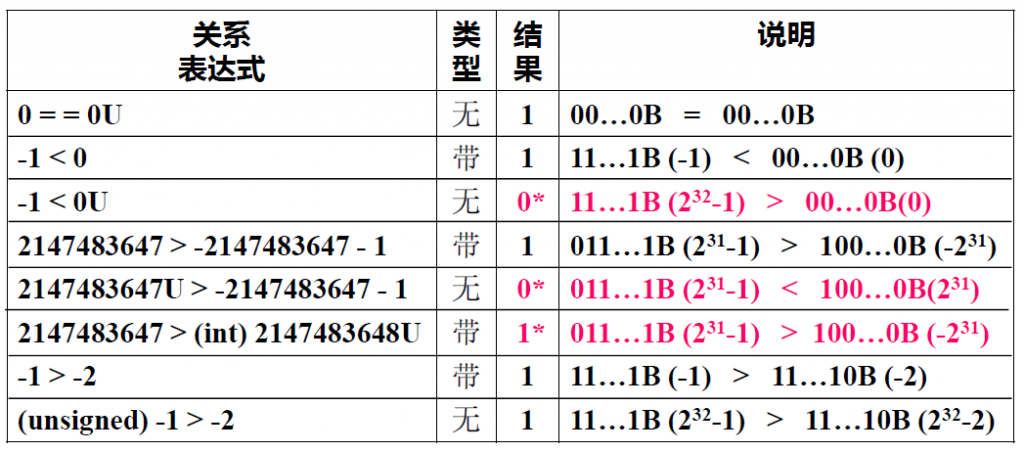
其中标红的就是结果不符合直觉的例子,上面三个不符合直觉的例子分析如下:
- 由于0是unsigned类型的,所以-1也会被转换成unsigned,而其补码是32个1,被解析成无符号整数后就是\(2^{31}-1\)
- 第五个也是一样,右边的结果-2147483648的补码是首位1加上31个0,被解析成无符号数之后就是\(2^{31}\)
- 第六个例子中,2147483648U的补码同样也是首位的1加上31个0,但因为前面加上了一个(int)后,被转换成了一个带符号的整数,则在解释的时候就变成了\(-2^{31}\)
浮点数表示
在看这里之前,可以先去前面看看关于移码的知识,很简单,但是在这里要用到这玩意。
我们先来看看十进制的平凡表示,也就是科学计数法:

有了科学计数法,我们就可以表示出任意实数了,而在计算机中,无非就是把底数换成2:
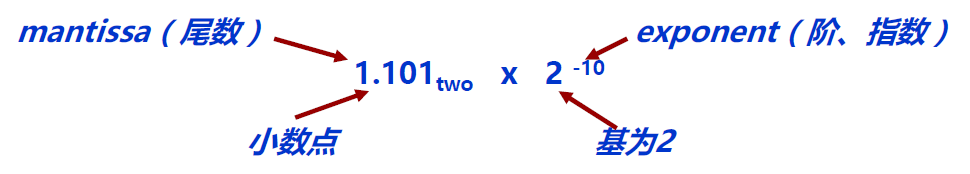
所以说,只要对尾数和指数分别编码,就可以得到一个浮点数(实数)
通常写成:\(X=\left( -1 \right) ^s\times M\times R^E\),在计算中,由于都是二进制表示的,所以R固定为2,所以说,确定了M和E,那么一个小数就确定了
而M的取值则可以有很多方式了,如让M的取值小于1且小数点后第一位为1,举个栗子,对于十进制的12.0,写成二进制是1100.0,相当于:\(0.11\times 2^4\),则可以得出s=0, M=0.11, R=2, E=4。
在IEEE 754标准中,定点小数M是一个值在1-2之间的数,比如说对于十进制12.0,写成二进制,相当于\(1.1\times 2^3\),则得出s=0, M=1.1, R=2, E=3。
浮点数在内存中一般是这样表示的(IEEE 754标准下 单精度):

- S:表示符号,0表示负数,1表示正数
- Exponent:表示阶码,也就是几次方
- 单精度规格化解码的范围为0000 0001到1111 1110(全零和全1用来表示特殊值)
- bias为127(单精度),1023(双精度)
- Significand:部分尾数,由于规格化尾数M是一个值在1-2之间的数,的最高位总是1,所以可以不表示出来,这样就可以节省一位。
浮点数的表示范围
在上面的图中,我们知道了S为符号,E(Exponent)表示阶码,M(significand)表示尾数,假设bias=128(注意这里不是IEEE754标准)
所以:
- 最大正数为:\(0.11\dots 1\times 2^{11\dots 1}=\left( 1-2^{-24} \right) \times 2^{127}\)
- 在这里解释一下,我们知道\(0.11\dots 1=1-0.00\dots 01\),所以括号里的东西应该不难理解,阶码为什么是127呢?这是因为:移码=bias+指数本身,而\(\text{移码}=11111111=255\),所以指数本身就等于255-bias = 255-128=127
- 最小正数位:\(0.10\dots 0\times 2^{00\dots 0}=\left( 1/2 \right) \times 2^{-128}\)
- 上面的补充看懂了下面的应该不难理解
因为原码是对称的,所以其表示的范围关于原点对称:

机器零:其实就是尾数为0或者在下溢区中的数。浮点数的范围比定点数大,但个数并没有变多,只是数与数之前变得更加稀疏,且不均匀。
将机器数转换成真值:
已知float型变量x的机器数是BEE00000H,求x的值:
首先将其转换成二进制:

$$
\left( -1 \right) ^s\times \left( 1+Significand \right) \times 2^{\left( Exponent-127 \right)}
$$
- 数符:1(负数)
- 阶:
- 阶码:001 1110 1 = 125
- 阶码的真值:阶码-bias = 125-127=-1
- 尾数:\(1+1\times 2^{-1}+1\times 2^{-2}+0\times 2^{-3}+1\times 2^{-4}+1\times 2^{-5}+\dots =1.75\)
- 真值:\(-1.75\times 2^{-2}=-0.4375\)
将真值转换成机器数:
已知float类型的变量x的值为-12.75,求x的机器数:
\(-12.75=-1100.11=-1.10011\times 2^3\),阶为3,所以:
- 符号S = 1
- 阶码E = 127 + 3 = 128 + 2 = 10000010
- 部分尾数:100 1100 0000 0000 0000 0000
所以x的机器表示为:

其他形式数的一些表示
前面说过:我们通常用Exponent中全零和全1用来表示特殊值:
| Exponent | Significand | 特殊的数 |
| 0 | 0 | +/-0 |
| 0 | nonzero(非零) | 表示非规格化数 |
| 1-254 | 任意小数点前隐含1 | 规格化数 |
| 255 | 0 | +/-infinity(无穷) |
| 255 | nonzero | NaN(非数) |
0的表示:
- +0: 1 00000000 00000000000000000000000
- -0: 0 00000000 00000000000000000000000
无穷的表示:
- \(+\infty\):0 11111111 00000000000000000000000
- \(-\infty\): 1 11111111 00000000000000000000000
所谓的NaN(非数),也就是一些不能表示的数,比如说sqrt(-4.0) = NaN,0/0 =NaN
- 用指数部分全1,尾数部分非零来表示
非数值数据的编码表示
- 逻辑数据的编码表示
- 表示:用一位来表示,N位二进制数可表示N个逻辑数据
- 运算:按位进行,按位与之类的
- 识别:逻辑数据和数值数据在表示上一样,计算机依靠指令来识别
- 西文字符的编码表示
- 特点:只需对有限个字母和数字符号、标点符号等辅助字符编码,且所有字符总数不超过256个
- 表示:使用ASCII码表示
- 操作:字符串操作,比如比较之类的
- 汉字及国际字符的编码表示:
- 特点:数量多,表示麻烦
- 编码形式:一共有好几种:输入码、内码、字模点阵或轮廓描述
数据的基本宽度
比特是计算机中处理、存储和传输信息的最小单位,二进制信息最基本的计量单位是“字节”,在现代计算机中,存储器按字节编址,字节是最小的可寻址单位,如果以一个字节为排列单位,则LSB表示最低有效字节,MSB表示最高有效字节。
除了比特和字节之外,还经常用“字”作为单位,字节和字是两个完全不同的东西,字长一般表示数据通路的宽度,也就是CPU内部总线的宽度、运算器的位数、通用寄存器的宽度等,而字则是表示被处理的信息的单位
容量经常使用的单位:

通信中的宽带经常使用的单位:

大端与小端
大端与小端其实就是数据的字节在地址中是如何排列的:大端指的是 MSB(最高有效位) 所在的地址是数的地址,小端指的是 LSB(最高有效位) 所在的地址是数的地址。







Comments 2 条评论
头疼的浮点小数
@CarpeDime 浮点数我还没写完,其实不难,电路炸了。。。