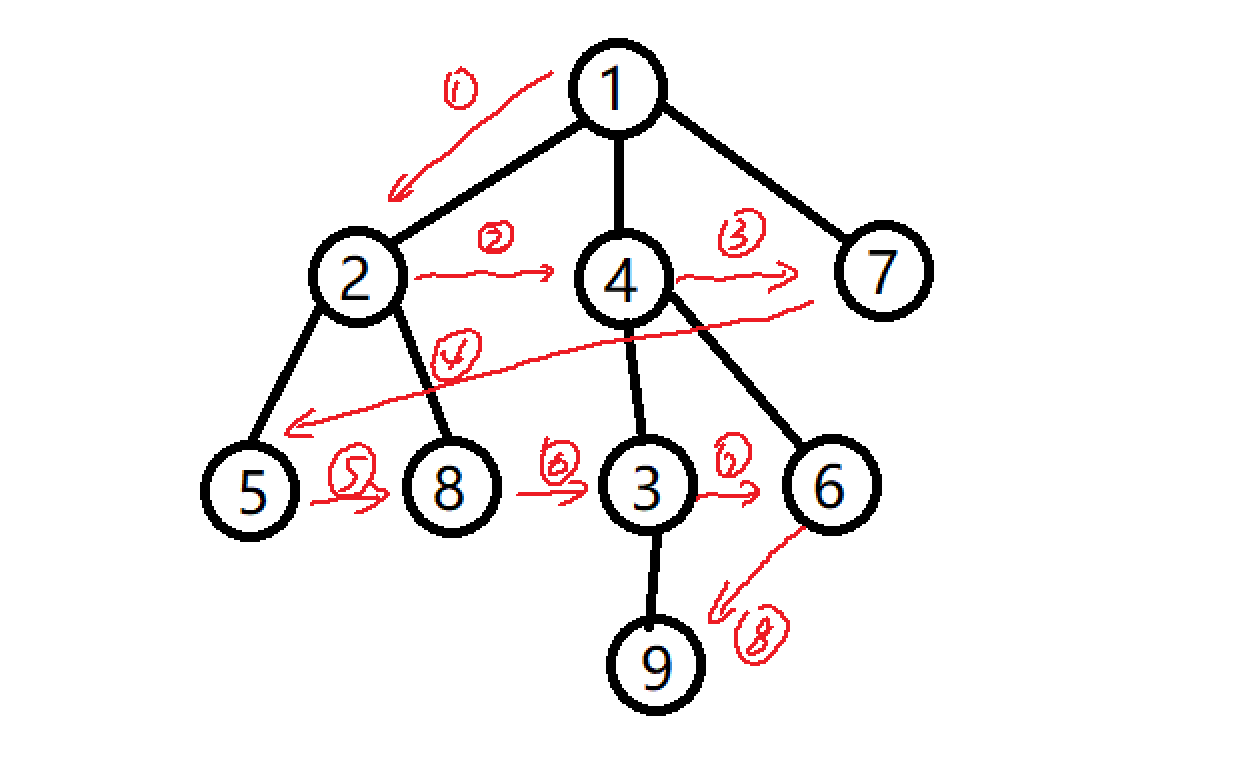
首先简单回顾一下dfs:在一个图中,首先找到一个点,依次从当前的点直接向未访问过的点进行扩展,如果发现当前点不可扩展了,那么向上返回上一个顶点,再进行搜索,直到所有的点都被访问完。(下面以一颗树为例)访问顺序:1->2->5->8->4->3->9->6->7

bfs:在一个图中,找到一个起点,先把离这个起点距离为1的点全部访问完,再访问距离为2的点...逐层扩展:
存储一个图
存储图可以使用邻接表或者邻接矩阵,但是邻接矩阵会浪费大量的空间,所以一般用的最多的就是邻接表,下面使用数组来模拟:
const int N = 10010;
int h[N], ne[N], e[N], idx; //使用数组模拟链表,h数组中的元素存的是图中的顶点,e数组存放的是节点的编号,ne[i]存的是i下标所对应的节点的下一个节点编号。
void add(int a, int b) { //建立a到b的关系
e[idx] = b; //节点b的编号就是当前的idx
ne[idx] = h[a]; //b指向表头后的元素
h[a] = idx++; //表头指向b,并将idx++
}dfs应用:树的重心
给定一颗树,树中包含n个结点(编号1~n)和n-1条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式:
第一行包含整数n,表示树的结点数。
接下来n-1行,每行包含两个整数a和b,表示点a和点b之间存在一条边。
输出格式:
输出一个整数m,表示重心的所有的子树中最大的子树的结点数目。
数据范围:
\(1\leqslant n\leqslant 10^5\)
输入样例:
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例:
4
分析:
首先如果我们删除1这个节点:

则会出现3个连通块,联通块中的点数分别是:3,4,1那么最大的点数就是4了
如果我们删除2这个节点:
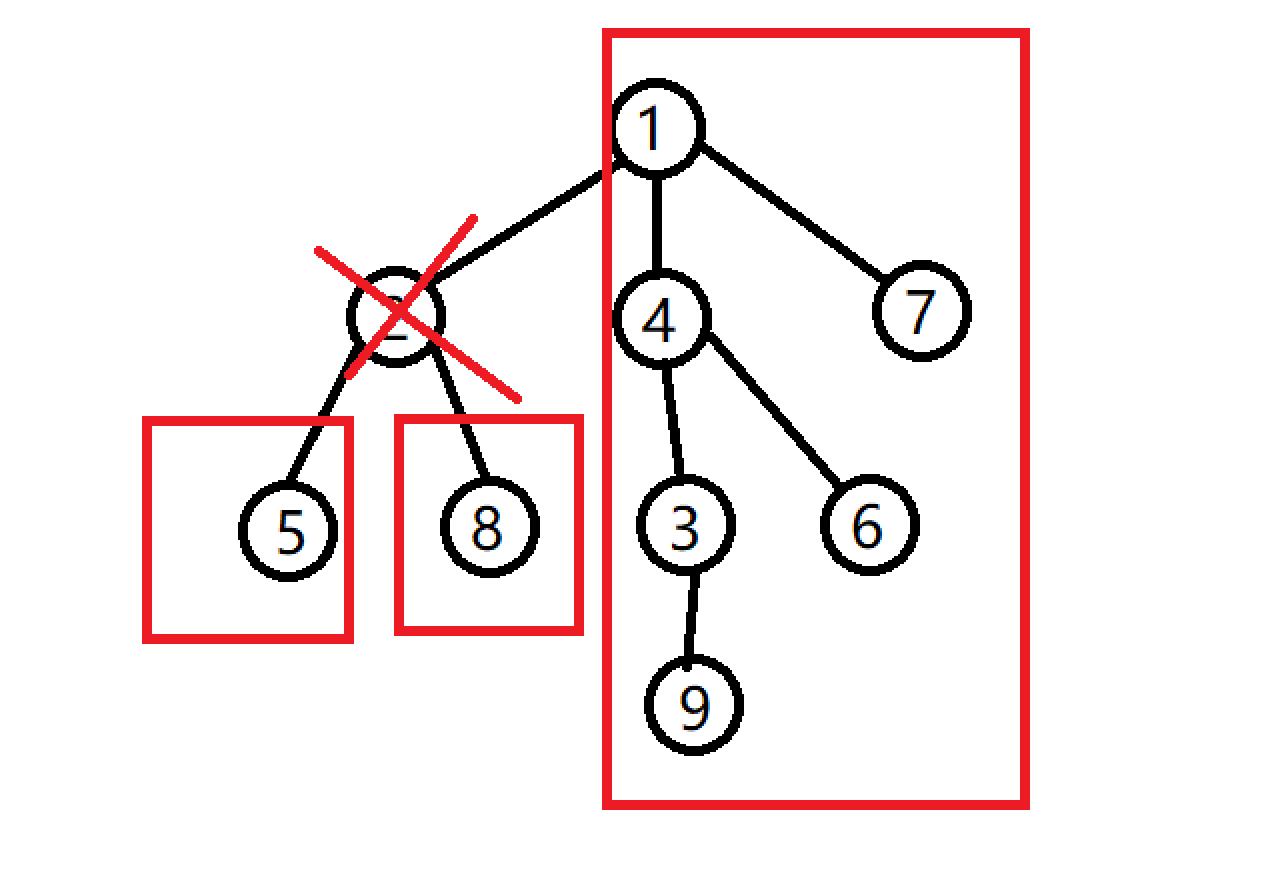
会出现3个连通块,联通块中的点数分别是:1,1,6那么最大的点数就是6了
再来,如果我们删除4这个点:
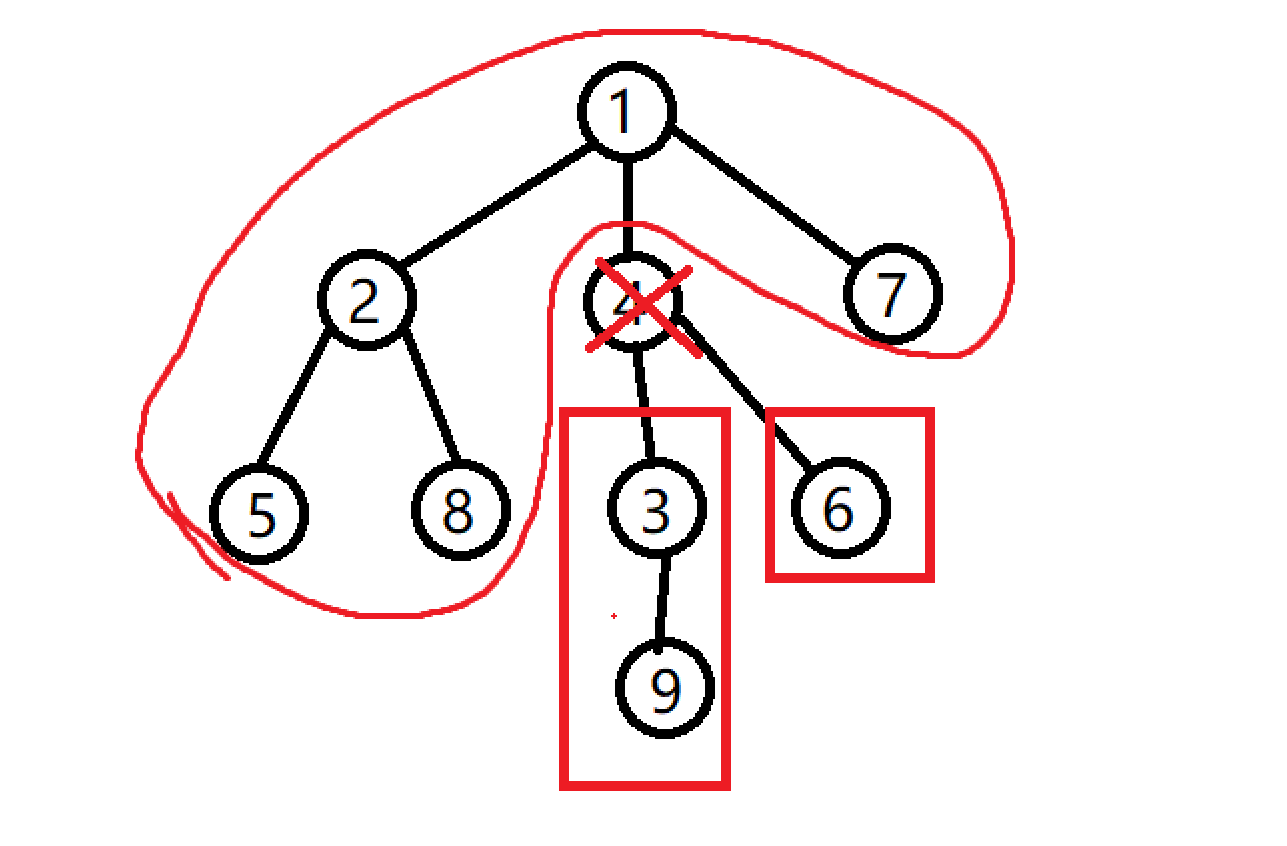
也会出现3个联通块连通块,连通块中的点数分别是5,2,1那么最大的点数就是5了
最后我们只需要对这些最大的点数求一个最小就行了,所以现在的问题被转换成了如何求那个最大的连通块。
由于dfs会把一个点的儿子全部都遍历一遍,所以可以根据这个特性求出子树的大小。还有一种特殊的情况就是当我们删除4这个节点的时候,可以看出,它的顶上还有一坨节点,这个直接求是很复杂的,但是我们可以用所有的节点,减去4这个点所含节点的个数,所以我们在深搜的过程中,还需要保存以当前节点为根的子树的大小。
示例代码如下:
#include<t;iostream>
#include<cstring>
using namespace std;
const int N = 10010;
int h[N], ne[N], e[N], idx, n;
bool vis[N];
int ans = N;
void add(int a, int b) { //添加节点
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int dfs(int k) { //以当前节点k为根的子树
vis[k] = true; //首先标记是这个节点为访问过的
int size = 1, res = 0; //这个节点本身算一个节点,所以size从1开始,res就是存的当前最大连通块中点的个数
for(int i = h[k]; i != -1; i = ne[i]) { //开始搜索每一个有关系的节点
int j = e[i];
if(!vis[j]) {
int s = dfs(j); //保存以j为根的子树的大小
size += s; //当前节点的大小要加上子树的大小
res = max(res, s); //更新最大的连通块
}
}
res = max(res, n - size); //最后还有一种特殊情况就是顶上有一坨的
ans = min(ans, res); //在最大的连通块中,选最小的
return size; //将当前子树的大小返回
}
int main(){
cin >> n;
memset(h, -1, sizeof h);
for(int i = 0; i < n - 1; ++i) {
int a, b;
cin >> a >> b;
add(a, b); //由于是无向图,所以既要建立a和b之间的关系
add(b, a); //也要建立b和a之间的关系
}
dfs(1);
cout << ans << endl;
return 0;
}bfs应用:图中点的层次
给定一个n个点m条边的有向图,图中可能存在重边和自环。
所有边的长度都是1,点的编号为1~n。
请你求出1号点到n号点的最短距离,如果从1号点无法走到n号点,输出-1。
输入格式
第一行包含两个整数n和m。
接下来m行,每行包含两个整数a和b,表示存在一条从a走到b的长度为1的边。
输出格式:
输出一个整数,表示1号点到n号点的最短距离。
数据范围:
n和m均为1到10的5次方
输入样例:
4 5
1 2
2 3
3 4
1 3
1 4
输出样例:
1
bfs的特性:层层扩展,所以一个点如果离起点越近,那么它就越早被访问到,所以说bfs是自带最短路特性的,如果要求a点到b点的最短距离,直接bfs就可以求出
示例代码:
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100010;
int e[N], ne[N], h[N], idx; //数组模拟效率高
int d[N]; //表示到起点的距离
int n, m;
queue<int> que;
void add(int a, int b) { //加点
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int bfs() {
memset(d, -1, sizeof d); //初始将所有点到起点的距离设置为-1
d[1]= 0; //起点到起点的距离为0,因为后面要用到,所以需要初始化
que.push(1); //将1号点加入队列
while(que.size()) { //只要队列里面还有元素,说明这一层的元素还没有遍历完
int t = que.front(); //保留起点元素
que.pop(); //起点元素被踢出队列,表示已经访问过了
for(int i = h[t]; i != -1; i = ne[i]) { //开始对起点元素扩展,跟他有关的全部加入加入队列
int j = e[i];
if(d[j] == -1) { //如果没有访问过
d[j] = d[t] + 1; //那就在上一个点的基础上加一步
que.push(j); //同时压入队列,准备后面的扩展
}
}
}
return d[n]; //访问完后,直接将第n个元素到起点的距离返回
}
int main(){
cin >> n >> m;
memset(h, -1, sizeof h);
while(m--) {
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
return 0;
}






Comments NOTHING